练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    关于x的函数y=（m+1）x2+（m-1）x+m，当m=0时，它是    函数；当m=-1时，它是    函数．
    【答案】分析：把m=0，m=-1分别代入函数关系式，再根据函数的定义来判断．
    解答：解：当m=0时，函数解析式变化成y=x2-x，是一个二次函数；
    当m=-1时，函数变化成y=-2x-1，是一次函数．
    点评：本题主要考查一次函数与二次函数的定义与一般形式．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

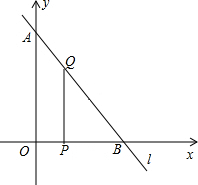    （2009•南安市质检）如图，在直角坐标系中，已知点A（0，6），B（8，0）．
    （1）直接写出AB的长；
    （2）点P（x，0）为线段OB上一动点（点O、B除外），过点P作PQ∥OA交AB于点Q．
    ①若以线段PQ为直径的⊙M与y轴相切，求点P的坐标；
    ②把△BPQ沿直线PQ向左侧翻折叠到△CPQ，若△CPQ与梯形OPQA重叠部分的面积为s，求s关于x的函数关系式，并求当x为何值时，s的值最大，最大值是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•荆门）为了节约资源，科学指导居民改善居住条件，小王向房管部门提出了一个购买商品房的政策性方案．
    人均住房面积（平方米） 单价（万元/平方米）
    不超过30（平方米） 0.3
    超过30平方米不超过m（平方米）部分（45≤m≤60） 0.5
    超过m平方米部分 0.7
    根据这个购房方案：
    （1）若某三口之家欲购买120平方米的商品房，求其应缴纳的房款；
    （2）设该家庭购买商品房的人均面积为x平方米，缴纳房款y万元，请求出y关于x的函数关系式；
    （3）若该家庭购买商品房的人均面积为50平方米，缴纳房款为y万元，且57＜y≤60 时，求m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•荆门）如图1，正方形ABCD的边长为2，点M是BC的中点，P是线段MC上的一个动点（不与M、C重合），以AB为直径作⊙O，过点P作⊙O的切线，交AD于点F，切点为E．
    （1）求证：OF∥BE；
    （2）设BP=x，AF=y，求y关于x的函数解析式，并写出自变量x的取值范围；
    （3）延长DC、FP交于点G，连接OE并延长交直线DC与H（图2），问是否存在点P，使△EFO∽△EHG（E、F、O与E、H、G为对应点）？如果存在，试求（2）中x和y的值；如果不存在，请说明理由．

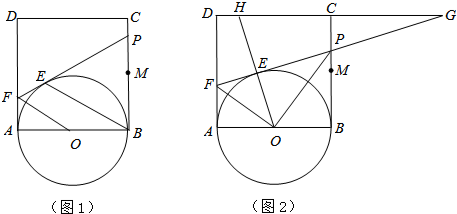
    查看答案和解析>>

    科目：初中数学 来源： 题型：

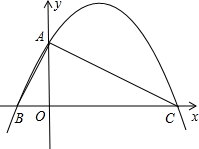    （2012•朝阳）已知，如图，在平面直角坐标系中，Rt△ABC的斜边BC在x轴上，直角顶点A在y轴的正半轴上，A（0，2），B（-1，0）．
    （1）求点C的坐标；
    （2）求过A、B、C三点的抛物线的解析式和对称轴；
    （3）设点P（m，n）是抛物线在第一象限部分上的点，△PAC的面积为S，求S关于m的函数关系式，并求使S最大时点P的坐标；
    （4）在抛物线对称轴上，是否存在这样的点M，使得△MPC（P为上述（3）问中使S最大时的点）为等腰三角形？若存在，请直接写出点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

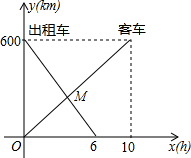    （2013•婺城区一模）一辆客车从甲地开往乙地，一辆出租车从乙地开往甲地，两车同时出发，设客车离甲地的距离为y1（km），出租车离甲地的距离为y2（km），客车行驶时间为x（h），y1，y2与x的函数关系图象如图所示：
    （1）根据图象，直接写出y1，y2关于x的函数关系式：y1=
    60x
    60x
    ，y2=
    -100x+600
    -100x+600
    ；
    （2）甲、乙两地间有A、B两个加油站，相距280km，若客车进入A站加油时，出租车恰好进入B站加油．求A加油站到甲地的距离．

    查看答案和解析>>

    同步练习册答案