
 如图,抛物线y=ax2+bx+c经过点A(-$\sqrt{3}$,0),B(3$\sqrt{3}$,0),C(0,-3)三点,线段BC与抛物线的对称轴l相交于点D,设抛物线的顶点为P,连接PA、AD、DP,线段AD与y轴相交于点E.
如图,抛物线y=ax2+bx+c经过点A(-$\sqrt{3}$,0),B(3$\sqrt{3}$,0),C(0,-3)三点,线段BC与抛物线的对称轴l相交于点D,设抛物线的顶点为P,连接PA、AD、DP,线段AD与y轴相交于点E.分析 (1)设抛物线解析式为y=a(x+$\sqrt{3}$)(x-3$\sqrt{3}$),把C(0,-3)代入即可解决问题.
(2)点Q位置存在4种情况;分类讨论①∠QCD=120°,QC=AD;②∠QCD=120°,QC=AD;③∠QDC=120°,QD=AD;④∠QDC=120°,QD=AD;即可解题.
(3)把(2)中的点Q坐标代入求出t的值即可判断.
解答 解:(1)设抛物线解析式为y=a(x+$\sqrt{3}$)(x-3$\sqrt{3}$),把C(0,-3)代入得a=$\frac{1}{3}$,
∴抛物线的解析式为y=$\frac{1}{3}$(x2-2$\sqrt{3}$x-9)=$\frac{1}{3}$x2-$\frac{2}{3}\sqrt{3}$x-3
∴抛物线解析式为y=$\frac{1}{3}$x2-$\frac{2}{3}\sqrt{3}$x-3.
(2)如图所示,
点Q位置存在4种情况;
连接AC,
∵tan∠OAC=$\frac{OC}{OA}$=$\sqrt{3}$,tan∠OBC=$\frac{OC}{OB}$=$\frac{\sqrt{3}}{3}$,
∴∠OAC=60°,∠OBC=30°,
∴∠OCB=60°,
∵DA=DB,
∴∠DAB=∠DBA=30°,
∴∠ADC=∠DAB+∠DBA=60°,
∵AE=2$\sqrt{3}$,DE=2,D($\sqrt{3}$,4),
∴DP=2,CD=CB-BD=6-4=2,
∴CD=DP,∵∠CDP=60°,
∴△CDP是等边三角形,
①当∠Q1CD=120°,QC=AD=4时,△Q1CD≌△ADP,
此时Q点在y轴上,则点Q1坐标(0,-7);
②当∠Q2DC=120°,Q2D=AD=4时,△Q2DC≌△ADP
此时Q2在对称轴上,Q2($\sqrt{3}$,2);
③当∠Q3DC=120°,DQ3=AD=4时,△Q3DC≌△ADP,
此时Q2,Q3关于BC对称,Q3(3$\sqrt{3}$,-4);
④当∠Q4CD=120°,Q4C=AD=4时,△Q4CD≌△ADP,
此时Q4,Q1关于BC对称,Q4(-2$\sqrt{3}$,-1);
(3)①点Q1坐标(0,-7)代入y=9(x-t)2-7得到t=0;
②点Q1坐标($\sqrt{3}$,2)代入y=9(x-t)2-7得到t=$\sqrt{3}$±1
③点Q1坐标(3$\sqrt{3}$,-4代入y=9(x-t)2-7得到t=$\frac{10\sqrt{3}}{3}$或$\frac{8\sqrt{3}}{3}$
④点Q1坐标(-2$\sqrt{3}$,-1);代入y=9(x-t)2-7得到t=-2$\sqrt{3}$+$\frac{\sqrt{6}}{3}$或-2$\sqrt{3}$-$\frac{\sqrt{6}}{3}$.
综上所述,点Q均在抛物线y=9(x-t)2-7外时,t≠0,t$≠\sqrt{3}±1$,t≠$\frac{10\sqrt{3}}{3}$,t≠$\frac{8\sqrt{3}}{3}$,t≠-2$\sqrt{3}±\frac{\sqrt{6}}{3}$.
点评 本题考查了特殊角的三角函数值,考查了三角函数在直角三角形中运用,本题考查了分类讨论思想,本题中根据全等三角形对应边相等性质求解是解题的关键,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
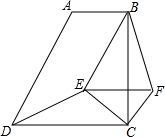 如图,直角梯形ABCD中,AB∥CD,∠DCB=90°,AB=5,BC=10,tan∠ADC=2.
如图,直角梯形ABCD中,AB∥CD,∠DCB=90°,AB=5,BC=10,tan∠ADC=2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
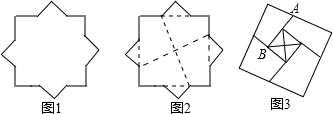
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{2}$-1 | D. | $\sqrt{2}$+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在Rt△ABC中,∠B=90°,∠A=30°,AC=2$\sqrt{3}$+2,四边形BDEF是△ABC的内接正方形(点D、E、F在三角形的边上).则此正方形的周长是4$\sqrt{3}$.
如图,在Rt△ABC中,∠B=90°,∠A=30°,AC=2$\sqrt{3}$+2,四边形BDEF是△ABC的内接正方形(点D、E、F在三角形的边上).则此正方形的周长是4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
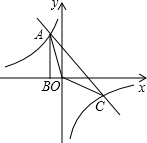 如图,Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=$\frac{3}{2}$.
如图,Rt△ABO的顶点A是双曲线y=$\frac{k}{x}$与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com