
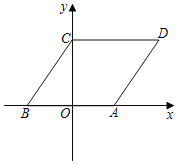
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌСтаЮABCDЕФБпABдкxжсЩЯЃЌЕуBзјБъЃЈЉ3ЃЌ0ЃЉЃЌЕуCзјБъЃЈ0ЃЌ4ЃЉЃЌЕуPДгдЕуOГіЗЂЃЌвдУПУывЛИіЕЅЮЛГЄЖШЕФЫйЖШбиxжсе§ЗНЯђвЦЖЏЃЌвЦЖЏЪБМфЮЊtЃЈ0ЁмtЁм5ЃЉУыЃЌЙ§ЕуPзїЦНаагкyжсЕФжБЯпlЃЌжБЯпlЩЈЙ§ЫФБпаЮOCDAЕФУцЛ§ЮЊSЃЎ
ЃЈ1ЃЉЧѓжБЯпADЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЕБSЃН![]() ЪБЃЌЧыжБНгаДГіtЕФжЕЃЛ
ЪБЃЌЧыжБНгаДГіtЕФжЕЃЛ
ЃЈ3ЃЉШчЙћЕуMЪЧЃЈ2ЃЉжаЕФжБЯп1ЩЯЕФЕуЃЌЕуNдкxжсЩЯЃЌВЂЧввдAЃЌDЃЌMЃЌNЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌЧыжБНгаДГіЕуNЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃН![]() xЉ
xЉ![]() ЃЛЃЈ2ЃЉtЕФжЕЮЊ4УыЃЛЃЈ3ЃЉЕуNзјБъЮЊЃЈ1ЃЌ0ЃЉЛђЃЈ3ЃЌ0ЃЉЛђЃЈ7ЃЌ0ЃЉЃЎ
ЃЛЃЈ2ЃЉtЕФжЕЮЊ4УыЃЛЃЈ3ЃЉЕуNзјБъЮЊЃЈ1ЃЌ0ЃЉЛђЃЈ3ЃЌ0ЃЉЛђЃЈ7ЃЌ0ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉдкRtЁїBOCжаЃЌРћгУЙДЙЩЖЈРэМЦЫуBCЕФГЄЃЌМДСтаЮЕФБпГЄЮЊ5ЃЌПЩЕУDКЭAЕФзјБъЃЌИљОнД§ЖЈЯЕЪ§ЗЈПЩНтД№ЃЛ
ЃЈ2ЃЉЂйШчЭМ1жаЃЌЕБ0ЁмtЁм2ЪБЃЌжБЯпlЩЈЙ§ЕФЭМЯѓЪЧЫФБпаЮCCQPЃЌSЃН4tЃЎЂкШчЭМ2жаЃЌЕБ2ЃМtЁм5ЪБЃЌжБЯпlЩЈЙ§ЕФЭМаЮЪЧЮхБпаЮOCQTAЃЎЗжБ№ЧѓНтМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉИљОнЬтвтЗжШ§жжЧщаЮЗжБ№зїЭМЃЌИљОнЦНааЫФБпаЮЕФаджЪМДПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉЁпЕуBзјБъЃЈЉ3ЃЌ0ЃЉЃЌЕуCзјБъЃЈ0ЃЌ4ЃЉЃЌ
ЁрOBЃН3ЃЌOCЃН4ЃЌ
дкRtЁїBOCжаЃЌBCЃН![]() ЃН
ЃН![]() ЃН5ЃЌ
ЃН5ЃЌ
ЁпЫФБпаЮABCDЪЧСтаЮЃЌ
ЁрCDЃНABЃНBCЃН5ЃЌ
ЁрAЃЈ2ЃЌ0ЃЉЃЌDЃЈ5ЃЌ4ЃЉЃЌ
ЩшADЕФНтЮіЪНЮЊЃКyЃНkx+bЃЌ
дђ![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК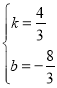 ЃЌ
ЃЌ
ЁржБЯпADЕФКЏЪ§БэДяЪНЮЊЃКyЃН![]() xЉ
xЉ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЂйШчЭМ1жаЃЌЕБ0ЁмtЁм2ЪБЃЌжБЯпlЩЈЙ§ЕФЭМЯѓЪЧЫФБпаЮOCQPЃЌSЃН4tЃЎ
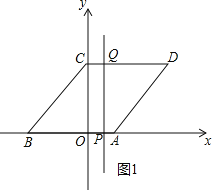
4tЃН![]() ЃЌtЃН
ЃЌtЃН![]() ЃО2ЃЌВЛЗћКЯЬтвтЃЛ
ЃО2ЃЌВЛЗћКЯЬтвтЃЛ
ЂкШчЭМ2жаЃЌЕБ2ЃМtЁм5ЪБЃЌжБЯпlЩЈЙ§ЕФЭМаЮЪЧЮхБпаЮOCQTAЃЎ
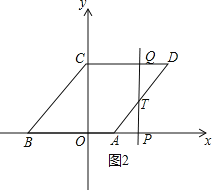
дђOPЃНtЃЌ
tanЁЯOBCЃНtanЁЯPATЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃЌPTЃН
ЃЌPTЃН![]() ЃЌ
ЃЌ
SЃНSОиаЮCOPQЉSЁїATPЃН4tЉ![]() ЁСЃЈtЉ2ЃЉЁС
ЁСЃЈtЉ2ЃЉЁС![]() ЃЈtЉ2ЃЉЃНЉ
ЃЈtЉ2ЃЉЃНЉ![]() t2+
t2+![]() tЉ
tЉ![]() ЃЌ
ЃЌ
ЕБSЃН![]() ЪБЃЌЉ
ЪБЃЌЉ![]() t2+
t2+![]() tЉ
tЉ![]() ЃН
ЃН![]() ЃЌ
ЃЌ
НтЕУЃКtЃН4Лђ6ЃЈЩсЃЉЃЌ
злЩЯЃЌЕБSЃН![]() ЪБЃЌtЕФжЕЮЊ4УыЃЛ
ЪБЃЌtЕФжЕЮЊ4УыЃЛ
ЃЈ3ЃЉДцдкШ§жжЧщПіЃК
ЂйШчЭМ3жаЃЌЫФБпаЮMNADЪЧЦНааЫФБпаЮЃЌДЫЪБMгыQжиКЯЃЌдђDMЃНANЃЌ
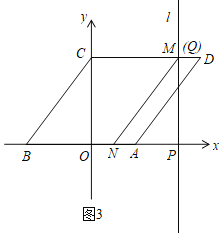
гЩЃЈ2ЃЉжЊЃКtЃН4ЃЌдђCMЃНOPЃН4ЃЌ
ЁрANЃНDMЃН5Љ4ЃН1ЃЌ
ЁрONЃН2Љ1ЃН1ЃЌ
ЁрNЃЈ1ЃЌ0ЃЉЃЛ
ЂкШчЭМ4ЃЌЫФБпаЮANDMЪЧЦНааЫФБпаЮЃЌдђDMЃНANЃЌЭЌРэЕУNЃЈ3ЃЌ0ЃЉЃЛ
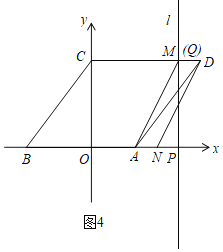
ЂлШчЭМ5ЃЌЫФБпаЮADNMЪЧЦНааЫФБпаЮЃЌдђADЃНMNЃН5ЃЌ
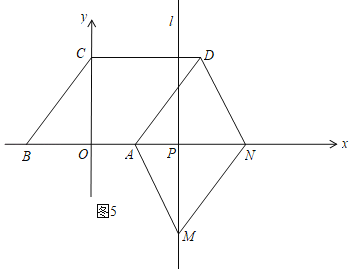
ЁпPMЃН4ЃЌ
RtЁїPMNжаЃЌPNЃН![]() =
=![]() =3ЃЌ
=3ЃЌ
ЁрONЃН4+3ЃН7ЃЌ
ЁрNЃЈ7ЃЌ0ЃЉЃЛ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕуNзјБъЮЊЃЈ1ЃЌ0ЃЉЛђЃЈ3ЃЌ0ЃЉЛђЃЈ7ЃЌ0ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌФГЖўДЮКЏЪ§ЕФЭМЯѓЪЧвЛЬѕЖЅЕуЮЊP(4ЃЎ-4)ЕФХзЮяЯпЃЌЫќОЙ§дЕуКЭЕуAЃЌЫќЕФЖдГЦжсНЛЯпЖЮ
OAгкЕуMЃЎЕуNдкЖдвЦжсЩЯЃЌЧвЕуMЁЂNЙигкЕуPЖдГЦЃЌСЌНгANЃЌON
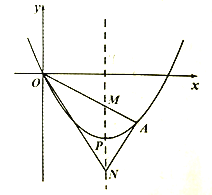
ЃЈ1ЃЉЧѓДЫЖўДЮКЏЪ§ЕФНтЮіЪНЃК
ЃЈ2ЃЉШєЕуAЕФзјБъЪЧ(6ЃЌ-3)ЃЎЃЌЧыжБНгаДГіMNЕФГЄ
ЃЈ3ЃЉШєЕуAдкХзЮяЯпЕФЖдГЦжсгвВрдЫЖЏЪБЃЌдђЁЯANMгыЁЯONMгаЪВУДЪ§СПЙиЯЕЃПВЂжЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕу![]() ЮЊЕШБп
ЮЊЕШБп![]() ЭтвЛЕуЃЌ
ЭтвЛЕуЃЌ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЕФГЄЮЊ_____________ЃЎ
ЕФГЄЮЊ_____________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
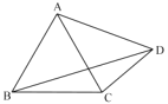
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкШёНЧШ§НЧаЮABCжаЃЌABЃН8ЃЌACЃН5ЃЌBCЃН6ЃЌбиЙ§ЕуBЕФжБЯпелЕўетИіШ§НЧаЮЃЌЪЙЕуCТфдкABБпЩЯЕФЕуEДІЃЌелКлЮЊBDЃЌЯТСаНсТлЃКЂйЁЯCBDЃНЁЯEBDЃЌЂкDEЁЭABЃЌЂлШ§НЧаЮADEЕФжмГЄЪЧ7ЃЌЂм![]() ЃЌЂн
ЃЌЂн![]() .Цфжае§ШЗЕФИіЪ§гаЃЈ ЃЉ
.Цфжае§ШЗЕФИіЪ§гаЃЈ ЃЉ
A.2B.3C.4D.5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
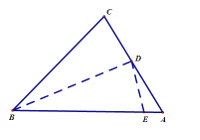
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+bxЉ![]() ОЙ§ЕуAЃЈЉ2ЃЌ
ОЙ§ЕуAЃЈЉ2ЃЌ![]() ЃЉЃЌгыxжсЯрНЛгкBЃЌCСНЕуЃЌЧвBЕузјБъЮЊЃЈЉ1ЃЌ0ЃЉЃЎ
ЃЉЃЌгыxжсЯрНЛгкBЃЌCСНЕуЃЌЧвBЕузјБъЮЊЃЈЉ1ЃЌ0ЃЉЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЕуDдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧвЮЛгкxжсЕФЩЯЗНЃЌНЋЁїBCDбижБЯпBDЗелЕУЕНЁїBCЁфDЃЌШєЕуCЁфЧЁКУТфдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧѓЕуCЁфКЭЕуDЕФзјБъЃЛ
ЃЈ3ЃЉХзЮяЯпгыyжсНЛгкЕуQЃЌСЌНгBQЃЌDQЃЌдкХзЮяЯпЩЯгавЛИіЖЏЕуPЃЌЧвSЁїPBDЃНSЁїBDQЃЌЧѓТњзуЬѕМўЕФЕуPЕФКсзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
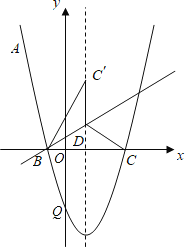
ЁОЬтФПЁПШчЭМЃЌдкУПИіаЁе§ЗНаЮЕФБпГЄЮЊ1ЕФЭјИёжаЃЌЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ОљдкИёЕуЩЯЃЌЕу
ОљдкИёЕуЩЯЃЌЕу![]() ЪЧдкжБЯп
ЪЧдкжБЯп![]() ЩЯЕФЖЏЕуЃЌСЌ
ЩЯЕФЖЏЕуЃЌСЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧЕу
ЪЧЕу![]() ЙигкжБЯп
ЙигкжБЯп![]() ЕФЖдГЦЕу.
ЕФЖдГЦЕу.
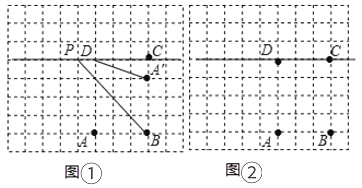
ЃЈ1ЃЉдкЭМЂйжаЃЌЕБ![]() ЃЈЕу
ЃЈЕу![]() дкЕу
дкЕу![]() ЕФзѓВрЃЉЪБЃЌМЦЫу
ЕФзѓВрЃЉЪБЃЌМЦЫу![]() ЕФжЕЕШгк______.
ЕФжЕЕШгк______.
ЃЈ2ЃЉЕБ![]() ШЁЕУзюаЁжЕЪБЃЌЧыдкШчЭМЂкЫљЪОЕФЭјИёжаЃЌгУЮоПЬЖШЕФжБГпЛГіЕу
ШЁЕУзюаЁжЕЪБЃЌЧыдкШчЭМЂкЫљЪОЕФЭјИёжаЃЌгУЮоПЬЖШЕФжБГпЛГіЕу![]() ЃЌВЂМђвЊЫЕУїЕу
ЃЌВЂМђвЊЫЕУїЕу![]() ЕФЮЛжУЪЧШчКЮевЕНЕФ.ЃЈВЛвЊЧѓжЄУїЃЉ
ЕФЮЛжУЪЧШчКЮевЕНЕФ.ЃЈВЛвЊЧѓжЄУїЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжмШеЃЌаЁЬЮДгМвбизХвЛЬѕБЪжБЕФЙЋТЗВНааШЅБЈЭЄПДБЈЃЌПДСЫвЛЖЮЪБМфКѓЃЌЫћАДдТЗЗЕЛиМвжаЃЌаЁЬЮРыМвЕФОрРыyЃЈЕЅЮЛЃКmЃЉгыЫћЫљгУЕФЪБМфtЃЈЕЅЮЛЃКminЃЉжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЌЯТСаЫЕЗЈжае§ШЗЕФЪЧ(ЁЁЁЁ)
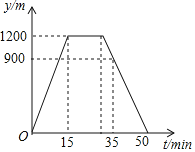
A. аЁЬЮМвРыБЈЭЄЕФОрРыЪЧ900m
B. аЁЬЮДгМвШЅБЈЭЄЕФЦНОљЫйЖШЪЧ60m/min
C. аЁЬЮДгБЈЭЄЗЕЛиМвжаЕФЦНОљЫйЖШЪЧ80m/min
D. аЁЬЮдкБЈЭЄПДБЈгУСЫ15min
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
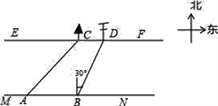
ЁОЬтФПЁПдкзлКЯЪЕМљПЮЩЯЃЌаЁДЯЫљдкаЁзщвЊВтСПвЛЬѕКгЕФПэЖШЃЌШчЭМЃЌКгАЖEFЁЮMNЃЌаЁДЯдкКгАЖMNЩЯЕуAДІгУВтНЧвЧВтЕУКгЖдАЖаЁЪїCЮЛгкЖЋББЗНЯђЃЌШЛКѓбиКгАЖзпСЫ30УзЃЌЕНДяBДІЃЌВтЕУКгЖдАЖЕчЯпИЫDЮЛгкББЦЋЖЋ30ЁуЗНЯђЃЌДЫЪБЃЌЦфЫћЭЌбЇВтЕУCD=10УзЃЎЧыИљОнетаЉЪ§ОнЧѓГіКгЕФПэЖШЃЎЃЈОЋШЗЕН0.1ЃЉЃЈВЮПМЪ§ОнЃК ![]() Ёж1.414ЃЌ
Ёж1.414ЃЌ ![]() Ёж1.132ЃЉ
Ёж1.132ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкRtЁїABCжаЃЌЁЯA=90ЁуЃЌAB=AC=![]() +2ЃЌDЪЧБпACЩЯЕФЖЏЕуЃЌBDЕФДЙжБЦНЗжЯпНЛBCгкЕуEЃЌСЌНгDEЃЌШєЁїCDEЮЊжБНЧШ§НЧаЮЃЌдђBEЕФГЄЮЊ_____ЃЎ
+2ЃЌDЪЧБпACЩЯЕФЖЏЕуЃЌBDЕФДЙжБЦНЗжЯпНЛBCгкЕуEЃЌСЌНгDEЃЌШєЁїCDEЮЊжБНЧШ§НЧаЮЃЌдђBEЕФГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com