
分析 (1)利用非负数的性质可求得a、b的值,根据三角形三边关系可求得c的范围;
(2)分腰长为3或4两种情况进行计算;
(3)分这两个内角一个为顶角和两个都是底角三种情况,结合三角形内角和定理可求得x,可得出三个角的度数.
解答 解:(1)∵|a-3|+(b-4)2=0,
∴a=3 b=4,
∵b-a<c<b+a,
∴1<c<7;
(2)当腰长为3时,此时三角形的三边为3、3、4,满足三角形三边关系,周长为10;
当腰长为4时,此时三角形的三边长为4、4、3,满足三角形三边关系,周长为11;
综上可知等腰三角形的周长为10或11;
(3)当底角为x°、顶角为(2x-20)°时,则根据三角形内角和为180°可得
x+x+2x-20=180,
解得x=50,
此时三个内角分别为50°、50°、80°;
当顶角为x°、底角为(2x-20)°时,则根据三角形内角和为180°可得
x+2x-20+2x-20=180,
解得x=44,
此时三个内角分别为44°、68°、68°;
当底角为x°、(2x-20)°时,则等腰三角形性质可得
x=2x-20,
解得x=20,
此时三个内角分别为20°、20°、140°;
综上可知三角形三个内角为50度、50度、80度或44度、68度、68度或20度、20度、140度.
点评 本题主要考查等腰三角形的性质,掌握等腰三角形的两腰相等、两底角相等是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 线段比直线长 | |
| B. | 过同一平面内的两点,可以作三条直线 | |
| C. | 一条射线有两个端点 | |
| D. | 两点之间的所有连线中,线段最短 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
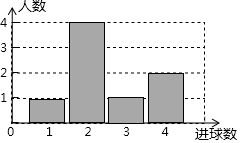 体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com