
 与直线y=x交于点A,点B在直线
与直线y=x交于点A,点B在直线 上,∠BOA=90°.抛物线
上,∠BOA=90°.抛物线 过点A,O,B,顶点为点E.
过点A,O,B,顶点为点E.
 与直线y=x交于点A,得
与直线y=x交于点A,得 ,解得,
,解得, 。
。 上,∴
上,∴ ,解得,
,解得,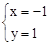 。
。 过点A,O,B,
过点A,O,B, ,解得,
,解得, 。
。 。
。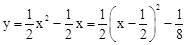 ,∴顶点E的坐标是(
,∴顶点E的坐标是( ,
, )。
)。 。
。 ,
, )。
)。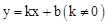 ,把B(﹣1,1),C(
,把B(﹣1,1),C( ,
, )代入,得
)代入,得 ,解得,
,解得, 。
。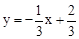 。
。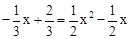 ,解得,x1=
,解得,x1=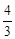 ,x2=﹣1.。
,x2=﹣1.。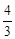 代入
代入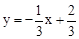 ,得y1=
,得y1= ,∴点D的坐标是(
,∴点D的坐标是(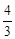 ,
, )。
)。

 ,
, ),
), 。
。 代入
代入 ,得x=
,得x=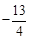 ,
,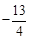 ,
, ),
),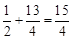 。
。 ,∴
,∴ 。
。 与直线y=x交于点A,列出方程组
与直线y=x交于点A,列出方程组 ,通过解该方程组即可求得点A的坐标;根据∠BOA=90°得到直线OB的解析式为y=﹣x,则
,通过解该方程组即可求得点A的坐标;根据∠BOA=90°得到直线OB的解析式为y=﹣x,则 ,通过解该方程组来求点B的坐标即可。
,通过解该方程组来求点B的坐标即可。

科目:初中数学 来源:不详 题型:单选题
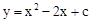 与y轴的交点为(0,﹣3),则下列说法不正确的是【 】
与y轴的交点为(0,﹣3),则下列说法不正确的是【 】| A.抛物线开口向上 |
| B.抛物线的对称轴是x=1 |
| C.当x=1时,y的最大值为﹣4 |
| D.抛物线与x轴的交点为(-1,0),(3,0) |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
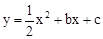 与y轴交于点C(0,-4),与x轴交于点A,B,且B点的坐标为(2,0)
与y轴交于点C(0,-4),与x轴交于点A,B,且B点的坐标为(2,0)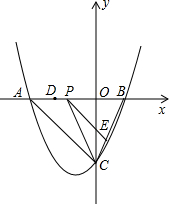
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 经过点A(x1,0),B(x2,0),C(0,-2),其顶点为D.以AB为直径的⊙M交y轴于点E、F,过点E作⊙M的切线交x轴于点N。∠ONE=30°,
经过点A(x1,0),B(x2,0),C(0,-2),其顶点为D.以AB为直径的⊙M交y轴于点E、F,过点E作⊙M的切线交x轴于点N。∠ONE=30°, 。
。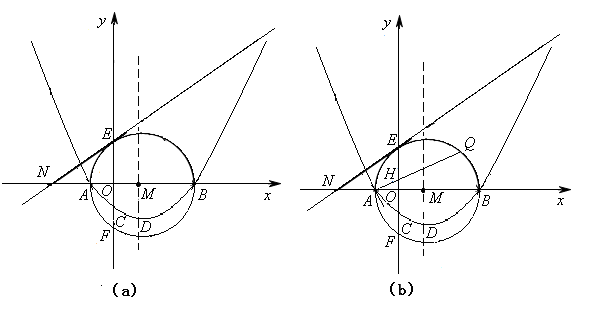
 上的动点(Q不与E、F重合),连结AQ交y轴于点H,问:AH·AQ是否为定值?若是,请求出这个定值;若不是,请说明理由。
上的动点(Q不与E、F重合),连结AQ交y轴于点H,问:AH·AQ是否为定值?若是,请求出这个定值;若不是,请说明理由。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
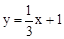 与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.
与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.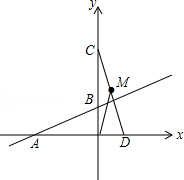
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
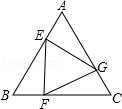
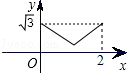 B.
B. C.
C.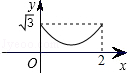 D.
D.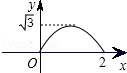
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com