练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

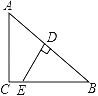
    【题目】如图，在△ABC中，∠ACB=90°，AC=6，AB=10，AB的垂直平分线DE交AB于点D，交BC于点E，则CE的长等于_____．

    【答案】

    【解析】连接AE，由垂直平分线的性质可得AE=BE，利用勾股定理可得BC=8，设CE=x，则BE=8-x，在△ACE中利用勾股定理可得x的长，即得ce的长.

    解：连接AE，

    ∵DE为AB的垂直平分线，

    ∴AE=BE，

    ∵在△ABC中，∠ACB=90°，AC=6，AB=10，

    由勾股定理得BC=8，

    设CE=x，则BE=8-x，在Rt△ACE中，

    由勾股定理得：x2+62=（8-x）2，

    解得x=，

    故答案为： .

    “点睛”本题主要考查了垂直平分线的性质和勾股定理，利用方程思想是解答此题的关键.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为了鼓励市民节约用水，某市居民生活用水按阶梯式水价计费。下表是该市民居民“一户一表”生活用水阶梯式计费价格表的部分信息：

    （说明：①每户产生的污水量等于该户自来水用水量；②水费=自来水费用+污水处理费）

    已知小王家2012年4月用水20吨，交水费66元，5月份用水25吨，交水费91元。

    （1）求a，b的值；

    （2）随着夏天的到来，用水量将增加。为了节省开支。小王计划把6月份的水费控制在不超过家庭月收入的2%，若小王家的月收入为9200元，则小王家6月份最多能用水多少吨？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面四个判断中正确的是（　　）.

    A. 过圆内一点（非圆心）的无数条弦中，有最长的弦，没有最短的弦

    B. 过圆内一点（非圆心）的无数条弦中，有最短的弦，没有最长的弦

    C. 过圆内一点（非圆心）的无数条弦中，有且只有一条最长的弦，也有且只有一条最短的弦

    D. 过圆内一点（非圆心）的无数条弦中，既没有最长的弦，也没有最短的弦

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知抛物线y=x2+bx+c（b，c为常数）的顶点为P，等腰直角三角形ABC的顶点A的坐标为（0，﹣1），C的坐标为（4，3），直角顶点B在第四象限．

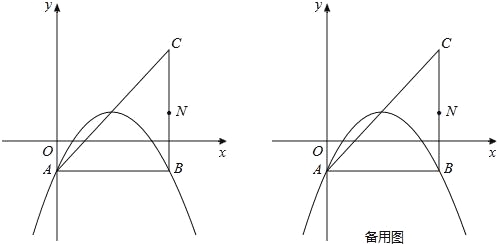
    （1）如图，若该抛物线过A，B两点，求该抛物线的函数表达式；

    （2）平移（1）中的抛物线，使顶点P在直线AC上滑动，且与AC交于另一点Q．

    （i）若点M在直线AC下方，且为平移前（1）中的抛物线上的点，当以M、P、Q三点为顶点的三角形是等腰直角三角形时，求出所有符合条件的点M的坐标；

    （ii）取BC的中点N，连接NP，BQ．试探究是否存在最大值？若存在，求出该最大值；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】两个城镇A、B与两条公路ME，MF位置如图所示，其中ME是东西方向的公路．现电信部门需在C处修建一座信号发射塔，要求发射塔到两个城镇A、B的距离必须相等，到两条公路ME，MF的距离也必须相等，且在∠FME的内部．

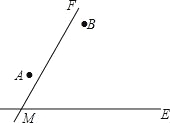
    （1）点C应选在何处？请在图中，用尺规作图找出符合条件的点C．（不写已知、求作、作法，只保留作图痕迹）

    （2）点C到公路ME的距离为2km，设AB的垂直平分线交ME于点N，点M处测得点C位于点M的北偏东60°方向，在N处没得点C位于点N的北偏西45°方向，求MN的长（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的一元二次方程（m+2）x2+mx+m2﹣4=0有一个根是0，则m= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表所示:

    成绩(m)

    1.50

    1.60

    1.65

    1.70

    1.75

    1.80

    人数(人)

    1

    2

    4

    3

    3

    2

    这些运动员跳高成绩的中位数和众数分别是（ ）

    A.1.70m，1.65mB.1.70m，1.70mC.1.65m，1.65mD.3人，4人

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一元二次方程x2－6x＋c＝0有一个根为2，则另一根为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】正式排球比赛时对所使用的排球质量有严格的规定，检查5个排球的重量，超过规定重量的数记作正数，不足规定重量的克数记作负数，检查结果如下：

    ＋15，－10，＋30，－20，－40.

    指出哪个排球质量好一些(即重量接近规定重量)，怎样用学过的绝对值的知识说明哪个排球的质量好一些？

    查看答案和解析>>

    同步练习册答案