
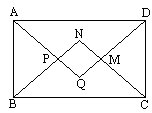
如图所示,已知:![]() ABCD中,角平分线AQ、BN、CN、DQ分别交于P,M,在不添加其他条件的情况下,试写出一个由上述条件推出来的结论.并给出证明过程(要求推理过程中要用到“平行四边形”和“角平分线”这两个条件).
ABCD中,角平分线AQ、BN、CN、DQ分别交于P,M,在不添加其他条件的情况下,试写出一个由上述条件推出来的结论.并给出证明过程(要求推理过程中要用到“平行四边形”和“角平分线”这两个条件).
|
解:这是一个探求结论的问题,它要求答题者开动脑筋,将已知条件和探求的要求联系起来,寻找出最适合作自己证明的结论.(1)若由平行四边形得AD∥BC,又AP,BP是角平分线,得到最简单又符合探求条件的结论:AQ⊥BN.(2)更深一层的考虑到AB=CD,∠BAD=∠BCD,∠ABC=∠ADC,加之角平分线,你还能得到△BPA与△DMC旋转后完全重合,甚至更多. 由已知条件得出AQ⊥BN 理由如下:在 又因为AQ、BN分别平分∠BAD、∠ABC 所以∠BAQ+∠ABN= 所以∠APB= 所以AQ⊥BN 说明:像这样探求结论的命题,一般可以得出很多结论,在众多符合条件结论中,你应选择最适合你自己证明的结论作为你的答案. |


科目:初中数学 来源: 题型:
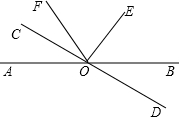 如图所示,已知直线AB和CD相交于点O,∠COE是直角,0F平分∠AOE.∠COF=34°.
如图所示,已知直线AB和CD相交于点O,∠COE是直角,0F平分∠AOE.∠COF=34°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com