
分析 先根据分式的混合运算顺序和法则化简原式,再将特殊锐角三角函数值代入求得x的值,代入求值即可得.
解答 解:原式=$\frac{(x+2)(x-2)}{x(x+2)^{2}}$÷$\frac{x-2}{x}$
=$\frac{x-2}{x(x+2)}$•$\frac{x}{x-2}$
=$\frac{1}{x+2}$,
当x=2(sin60°-tan45°)=2($\frac{\sqrt{3}}{2}$-1)=$\sqrt{3}$-2时,
原式=$\frac{1}{\sqrt{3}-2+2}$=$\frac{\sqrt{3}}{3}$.
点评 本题主要考查分式的化简求值和特殊锐角的三角函数值,熟练掌握分式的混合运算顺序和法则是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
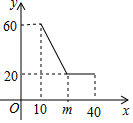 经市场调查,某公司生产的大白公仔的每天的销售量y(件)与销售价格x(元/件)之间的函数关系如图所示.
经市场调查,某公司生产的大白公仔的每天的销售量y(件)与销售价格x(元/件)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
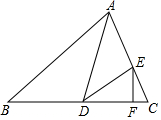 如图,在△ABC中,∠B=50°,AD平分∠CAB,交BC于D,E为AC边上一点,连接DE,∠EAD=∠EDA,EF⊥BC于点F.求∠FED的度数.
如图,在△ABC中,∠B=50°,AD平分∠CAB,交BC于D,E为AC边上一点,连接DE,∠EAD=∠EDA,EF⊥BC于点F.求∠FED的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 尺规作图并说明作图依据
尺规作图并说明作图依据查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com