
分析 (1)直接利用负整数指数幂的性质以及利用二次根式的性质和绝对值的性质和特殊角的三角函数值分别化简求出答案;
(2)直接去括号,利用分式乘法运算法则化简,进而通分化简,再将已知代入求出答案.
解答 解:(1)$\sqrt{12}$+2-1-|$\sqrt{3}$-2|-3tan60°
=2$\sqrt{3}$+$\frac{1}{2}$-(2-$\sqrt{3}$)-3×$\sqrt{3}$
=-$\frac{3}{2}$;
(2)x•($\frac{1}{x}$-$\frac{1}{x+1}$)
=1-$\frac{x}{x+1}$
=$\frac{1}{x+1}$,
把x=$\sqrt{5}$-1代入上式可得:原式=$\frac{1}{\sqrt{5}-1+1}$=$\frac{\sqrt{5}}{5}$.
点评 此题主要考查了实数运算以及分式的化简求值,正确掌握相关性质是解题关键.


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:解答题
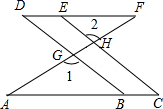 已知:如图,AC∥DF,直线AF分别与直线BD、CE相交于点G,H,∠1=∠2,求证:∠C=∠D.
已知:如图,AC∥DF,直线AF分别与直线BD、CE相交于点G,H,∠1=∠2,求证:∠C=∠D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3<a≤4 | B. | 2<a≤3 | C. | 2≤a<3 | D. | 3≤a<4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA的延长线上,∠FDA=∠B,AC=6,AB=8,则四边形AEDF的周长为( )
如图,在Rt△ABC中,∠BAC=90°,D、E分别是AB、BC的中点,F在CA的延长线上,∠FDA=∠B,AC=6,AB=8,则四边形AEDF的周长为( )| A. | 8 | B. | 16 | C. | 10 | D. | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
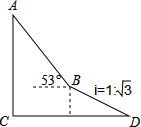 如图,为了测量出楼房AC的高度,从距离楼底C处60$\sqrt{3}$米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:$\sqrt{3}$的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈$\frac{4}{3}$,计算结果用根号表示,不取近似值).
如图,为了测量出楼房AC的高度,从距离楼底C处60$\sqrt{3}$米的点D(点D与楼底C在同一水平面上)出发,沿斜面坡度为i=1:$\sqrt{3}$的斜坡DB前进30米到达点B,在点B处测得楼顶A的仰角为53°,求楼房AC的高度(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈$\frac{4}{3}$,计算结果用根号表示,不取近似值).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com