
| 区县 | 大兴 | 通州 | 平谷 | 顺义 | 怀柔 | 门头沟 | 延庆 | 昌平 | 密云 | 房山 |
| 最高气温 | 32 | 32 | 30 | 32 | 30 | 32 | 29 | 32 | 30 | 32 |
| A. | 32 | B. | 31 | C. | 30 | D. | 29 |
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:选择题
| A. | 该函数图象经过点(-1,1) | B. | 该函数图象在第二、四象限 | ||
| C. | 当x<0时,y随着x的增大而减小 | D. | 当x>1时,-1<y<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
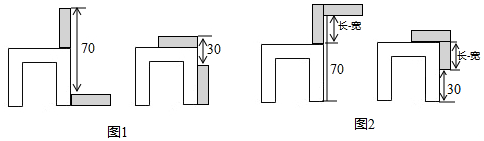
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
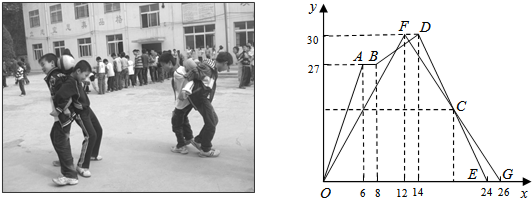
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
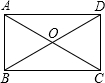 如图,矩形ABCD的两条对角线的一个交角为60o,两条对角线的长度的和为24cm,则这个矩形中AB的长为( )
如图,矩形ABCD的两条对角线的一个交角为60o,两条对角线的长度的和为24cm,则这个矩形中AB的长为( )| A. | 12cm | B. | 8cm | C. | 5cm | D. | 6cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com