
����Ŀ����ͼ�ף�ֱ��y=��x+3��x�ᡢy��ֱ��ڵ�B����C������B��C�����������y=x2+bx+c��x�����һ������ΪA������ΪP��
��1����������ߵĽ���ʽ��
��2���ڸ������ߵĶԳ������Ƿ���ڵ�M��ʹ��C��P��MΪ�����������Ϊ���������Σ������ڣ���ֱ��д�������������ĵ�M�����ꣻ�������ڣ���˵�����ɣ�
��3����0��x��3ʱ��������������һ��E��ʹ��CBE����������ֵ��ͼ�ҡ�������ͼ̽������

���𰸡���1��y=x2��4x+3����2����2��![]() ����2��7����2����1+2
����2��7����2����1+2![]() ����2����1��2
����2����1��2![]() ������3��E��������
������3��E��������![]() ��
��![]() ��ʱ����CBE��������
��ʱ����CBE��������
��������
�����������1����ֱ�߽���ʽ�����B��C���꣬���ô���ϵ��������������߽���ʽ��
��2���������߽���ʽ�����P�����꼰�Գ��ᣬ�����M�����꣬��ʾ��MC��MP��PC�ij�����MC=MP��MC=PC��MP=PC����������ɷֱ�õ�����M������ķ��̣������M������ꣻ
��3����E��EF��x�ᣬ��ֱ��BC�ڵ�F����x���ڵ�D�������E�����꣬��ʾ��F������꣬��ʾ��EF�ij�����һ���ɱ�ʾ����CBE����������ö��κ��������ʿ������ȡ�����ֵʱE������꣮
�����������1����ֱ��y=��x+3��x�ᡢy��ֱ��ڵ�B����C��
��B��3��0����C��0��3����
��B��C������������߽���ʽ�ɵ� ![]() �����
�����![]() ��
��
�������߽���ʽΪy=x2��4x+3��
��2����y=x2��4x+3=��x��2��2��1��
�������߶Գ���Ϊx=2��P��2����1����
��M��2��t������C��0��3����
��MC=![]() ��MP=|t+1|��PC=
��MP=|t+1|��PC=![]() ��
��
�ߡ�CPMΪ���������Σ�
����MC=MP��MC=PC��MP=PC���������
����MC=MPʱ������![]() =|t+1|�����t=
=|t+1|�����t=![]() ����ʱM��2��
����ʱM��2��![]() ����
����
����MC=PCʱ������![]() =2
=2![]() �����t=��1����P���غϣ���ȥ����t=7����ʱM��2��7����
�����t=��1����P���غϣ���ȥ����t=7����ʱM��2��7����
����MP=PCʱ������|t+1|=2![]() �����t=��1+2
�����t=��1+2![]() ��t=��1��2
��t=��1��2![]() ����ʱM��2����1+2
����ʱM��2����1+2![]() ����2����1��2
����2����1��2![]() ����
����
���Ͽ�֪�������������ĵ�M��������Ϊ��2��![]() ����2��7����2����1+2
����2��7����2����1+2![]() ����2����1��2
����2����1��2![]() ����
����
��3����ͼ����E��EF��x�ᣬ��BC�ڵ�F����x���ڵ�D��
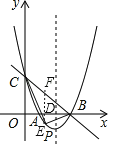
��E��x��x2��4x+3������F��x����x+3����
��0��x��3��
��EF=��x+3����x2��4x+3��=��x2+3x��
��S��CBE=S��EFC+S��EFB=![]() EFOD+
EFOD+![]() EFBD=
EFBD=![]() EFOB=
EFOB=![]() ��3����x2+3x��=��
��3����x2+3x��=��![]() ��x��
��x��![]() ��2+
��2+![]() ��
��
����x=![]() ʱ����CBE��������ʱE������Ϊ��
ʱ����CBE��������ʱE������Ϊ��![]() ��
��![]() ����
����
����E��������![]() ��
��![]() ��ʱ����CBE��������
��ʱ����CBE��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��ͼ��������![]() �У���
�У���![]() �ڶԽ���
�ڶԽ���![]() �ϣ���
�ϣ���![]() ��
��![]() ��
��![]() �����Բ.
�����Բ.

��1����֤��![]() ��
��![]() �����ߣ�
�����ߣ�
��2����![]() ��
��![]() �İ뾶.
�İ뾶.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
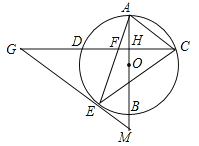
����Ŀ����ͼ��AB����O��ֱ������CD��AB������ΪH������AC����![]() ��һ��E��EG��AC��CD���ӳ����ڵ�G������AE��CD�ڵ�F����EG=FG������CE��
��һ��E��EG��AC��CD���ӳ����ڵ�G������AE��CD�ڵ�F����EG=FG������CE��
��1����֤����ECF�ס�GCE��
��2����֤��EG����O�����ߣ�
��3���ӳ�AB��GE���ӳ����ڵ�M����tanG=![]() ��AH=
��AH=![]() ����EM��ֵ��
����EM��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�½���ѧУ���������̻�У������꼶�ƻ�����![]() ��
��![]() ���ֻ�ľ��100���̻��ٳ�������
���ֻ�ľ��100���̻��ٳ�������![]() ��ľÿ��50Ԫ��
��ľÿ��50Ԫ��![]() ��ľÿ��100Ԫ.
��ľÿ��100Ԫ.
(1)������![]() ��
��![]() ������ľ�պ���ȥ8000Ԫ��������
������ľ�պ���ȥ8000Ԫ��������![]() ���ֻ�ľ�����ٿã�
���ֻ�ľ�����ٿã�
(2)�������![]() ��ľ������������
��ľ������������![]() ��ľ�������������һ�ֹ���ʹ�����ܷ�����ͣ�������ù��������ܷ��ã�
��ľ�������������һ�ֹ���ʹ�����ܷ�����ͣ�������ù��������ܷ��ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��һԪ���η�����
��һԪ���η�����![]() .
.
(1)��֤����������ʵ��![]() �����̶���ʵ������
�����̶���ʵ������
(2)��![]() Ϊ��ֵʱ�����̵���������Ϊ�෴������˵������.
Ϊ��ֵʱ�����̵���������Ϊ�෴������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����O�İ뾶Ϊ5cm����A��Բ��O�ľ���OA=3cm�����A��ԲO��λ�ù�ϵΪ��������
A.��A��Բ��
B.��A��Բ��
C.��A��Բ��
D.��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ͳ�������һ��������ƽ��ÿ��������ѩ���������ӣ�A��B��C��D��Eѩ��������������������£�A��133��B��182��C��68��D��39��E��98����B��ѩ����ֵ�Ƶ����(�� ��)
A. 5 B. 520
C. 182 D. 133
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ž�ͨ��·�IJ������ƣ�����������ҵ�ķ�չ��ij�����ξ�����A��B��C��D��E���������㣬�������β���ͳ�ƻ��Ƴ�2017�ꡰ��һ�������ڼ��������ͳ��ͼ������������Ϣ����������⣺

��1��2017�ꡰ��һ���ڼ䣬�����ܱ߾��㹲�Ӵ��ο� ���ˣ�����ͳ��ͼ��A��������Ӧ��Բ�ĽǵĶ����� ������ȫ����ͳ��ͼ��
��2�����ݽ����굽�������������������ƣ�Ԥ��2018�ꡰ��һ���ڽ���80���ο�ѡ��������Σ�������ж������˻�ѡ��ȥE�������Σ�
��3���ס���������������A��B��D���������У�ͬʱѡ��ȥͬһ����ĸ����Ƕ��٣����û���״ͼ���б�������˵�������о����õȿ��ܵĽ����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com