
【题目】 如图,在Rt△ABC中,∠C=90°,点O在边BC上,以点O为圆心,OB为半径的圆经过点A,过点A作直线AD,使∠CAD=2∠B.

(1)判断直线AD与⊙O的位置关系,并说明理由;
(2)若OB=4,∠CAD=60°,请直接写出图中弦AB与![]() 围成的阴影部分的面积.
围成的阴影部分的面积.
【答案】(1)直线AD与⊙O的位置关系是相切,理由见解析;(2)![]() -4
-4![]()
【解析】
(1)连接OA,根据等腰三角形的性质得到∠OAB=∠B,求得∠CAD=∠COA,推出OA⊥AD,于是得到结论;
(2)根据邻补角的定义得到∠AOB=120°,根据扇形和三角形的面积公式即可得到结论.
解:(1)直线AD与⊙O的位置关系是相切,
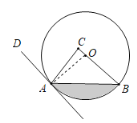
理由:连接OA,
∵OA=OB,
∴∠OAB=∠B,
∴∠COA=2∠B,
∵∠CAD=2∠B,
∴∠CAD=∠COA,
∵∠C=90°,
∴∠COA+∠OAC=90°,
∴∠CAO+∠CAD=90°,
∴∠OAD=90°,
∴OA⊥AD,
∴直线AD与⊙O相切;
(2)∵∠CAD=60°,
∴∠COA=∠CAD=60°,
∴∠AOB=120°,
∴∠B=∠OAB=30°,
∵OB=4
∴OA=OB=4
在Rt△OAC中,AC=OA·sin∠COA=2![]()
∴阴影部分的面积=S扇形AOB-S△AOB=![]() -
-![]() OB·AC=
OB·AC=![]() -4
-4![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 是
是![]() 上一点,且
上一点,且![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
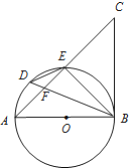
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,求证:
,求证:![]() 是
是![]() 的平分线;
的平分线;
(3)在(2)的条件下,延长![]() ,
,![]() 交与点
交与点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
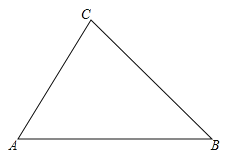
【题目】如图,已知△ABC,请用直尺(不带刻度),和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹).
(1)作菱形AMNP,使点M,N、P在边AB、BC、CA上;
(2)当∠A=60°,AB=8,AC=6时,求菱形AMNP的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
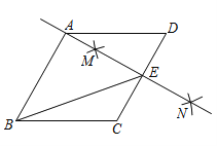
【题目】如图,在菱形ABCD中,按以下步骤作图:①分别以点C和点D为圆心,大于![]() 为半径作弧,两弧交于点M,N;②作直线MN,且
为半径作弧,两弧交于点M,N;②作直线MN,且![]() 恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )
恰好经过点A,与CD交于点E,连接BE,则下列说法错误的是( )
A.![]() B.
B.![]() C.若AB=4,则
C.若AB=4,则![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(14分)如图1,△ABC和△AED都是等腰直角三角形,∠BAC=∠EAD=90°,点B在线段AE上,点C在线段AD上.
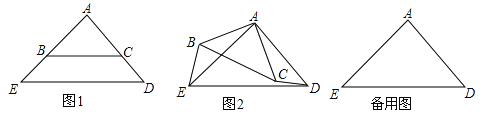
(1)请直接写出线段BE与线段CD的关系: ;
(2)如图2,将图1中的△ABC绕点A顺时针旋转角α(0<α<360°),
①(1)中的结论是否成立?若成立,请利用图2证明;若不成立,请说明理由;
②当AC=![]() ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,请直接写出角α的度数;若不存在,请说明理由.
ED时,探究在△ABC旋转的过程中,是否存在这样的角α,使以A、B、C、D四点为顶点的四边形是平行四边形?若存在,请直接写出角α的度数;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分6分)一只不透明的袋子中装有1个白球、1个蓝球和2个红球,这些球除颜色外都相同.
(1)从袋中随机摸出1个球,摸出红球的概率为 ;
(2)从袋中随机摸出1个球(不放回)后,再从袋中余下的3个球中随机摸出1个球,球两次摸到的球颜色不相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是⊙O上一点,OA⊥AB,且OA=1,AB=![]() ,OB交⊙O于点D,作AC⊥OB,垂足为M,并交⊙O于点C,连接BC.
,OB交⊙O于点D,作AC⊥OB,垂足为M,并交⊙O于点C,连接BC.
(1)求证:BC是⊙O的切线;
(2)过点B作BP⊥OB,交OA的延长线于点P,连接PD,求sin∠BPD的值.
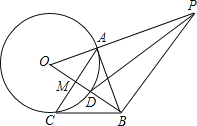
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了丰富学生课余生活,提高学生综合素质,开展了“综合实践活动课”,具体课程如下:A.数学史话;B.诗歌赏析:C.英语口语演讲;D.生物与生活,学校规定:每个学生都必须报名且只能选择其中的一个课程,学校随机抽查了部分学生,对他们选择的课程情况进行了统计,并绘制了如下两幅不完整的统计图.请结合统计图中的信息,解决下列问题:
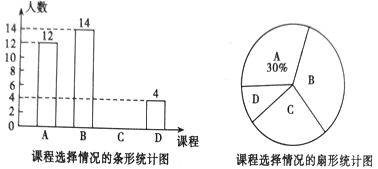
(1)这次学校抽查的学生人数是 ;课程B对应的扇形的圆心角是 度;
(2)将条形统计图补充完整;
(3)如果该校共有1200名学生,请你估计该校报D的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,点E在⊙O上,∠EAB的平分线交⊙O于点C,过点C作AE的垂线,垂足为D,直线DC与AB的延长线交于点P.
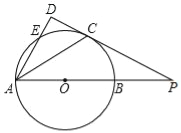
(1)判断直线PC与⊙O的位置关系,并说明理由;
(2)若tan∠P=![]() ,AD=6,求线段AE的长.
,AD=6,求线段AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com