
| A. | 3$\sqrt{3}$×5$\sqrt{3}$=15$\sqrt{3}$ | B. | 3$\sqrt{2}$$+2\sqrt{3}$=5$\sqrt{6}$ | C. | $\sqrt{8}$$-\sqrt{6}$=$\sqrt{2}$ | D. | $\sqrt{60}$$÷\sqrt{5}$=2$\sqrt{3}$ |
科目:初中数学 来源: 题型:解答题
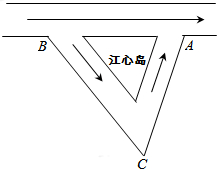 如图,已知箭头的方向是水流的方向,一艘游艇从江心岛的右侧A点逆流航行3小时到达B点后,又继续顺流航行2.5小时到达C点,总共行驶了208千米,已知游艇在静水中的速度是38千米/小时.
如图,已知箭头的方向是水流的方向,一艘游艇从江心岛的右侧A点逆流航行3小时到达B点后,又继续顺流航行2.5小时到达C点,总共行驶了208千米,已知游艇在静水中的速度是38千米/小时.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
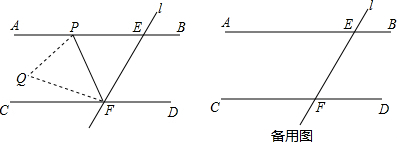
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
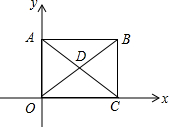 已知,矩形ABCO的对角线AC、BO相交于点D,△ADO是等边三角形,且A点的坐标为(0,2),则点D的坐标为($\sqrt{3}$,1).
已知,矩形ABCO的对角线AC、BO相交于点D,△ADO是等边三角形,且A点的坐标为(0,2),则点D的坐标为($\sqrt{3}$,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
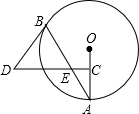 如图,AB是⊙O的弦,点C为半径OA的中点,过点C作CD⊥OA交弦AB于点E,连接BD,且DE=DB.
如图,AB是⊙O的弦,点C为半径OA的中点,过点C作CD⊥OA交弦AB于点E,连接BD,且DE=DB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com