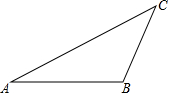
如图.已知:△ABC.请按下列要求用尺规作图(保留痕迹.不写作法及证明):(1)作AB边的垂直平分线l.垂足为点D,中所得直线l上.求作一点M.使点M到BC边所在直线的距离等于MD．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

2．

如图，已知：△ABC，请按下列要求用尺规作图（保留痕迹，不写作法及证明）：
（1）作AB边的垂直平分线l，垂足为点D；
（2）在（1）中所得直线l上，求作一点M，使点M到BC边所在直线的距离等于MD．

分析（1）根据中垂线的作图可得；
（2）作出∠ABC和其外角的角平分线，角平分线与直线l的交点即为所求作点．

解答解：（1）如图，直线l即为所求直线；

（2）如图，点M即为所求点．

点评本题主要考查作图-基本作图，熟练掌握中垂线的作图和角平分线的作图及其性质是解题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

12．

甲、乙两商场春节期间都进行让利酬宾活动，其中，甲商场对一次购物超过200元部分打7折（不超过200元部分按原价）优惠，如图所示，表示甲商场在让利方式下购物金额y（元）关于商品原价x（元）的函数图象；若乙商场所有商品按8折出售，请在同一坐标系下画出乙商场在让利方式下y关于x的函数图象，并利用图象说明如何选择这两家商场购物更省钱．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

13．已知a²-b²=14，其中（a+b）=2，则a-b=7．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

10．下列说法正确的是（　　）

	A．	最小的有理数是0
	B．	射线OM的长度是5cm
	C．	两数相加，和一定大于任何一个加数
	D．	两点确定一条直线

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

17．定义：如果a^b=N（a＞0，a≠1，N＞0），则b叫做以a为底N的对数，记作b=log_aN．
例如：求log₂8，因为2³=8，所以log₂8=3；又比如∵2^-3=$\frac{1}{8}$，∴${log}_{2}\frac{1}{8}$=-3
（1）根据定义计算：①log₃81=4；②log₁₀1=0；③如果log_x16=4，那么x=2．
（2）设a^x=M，a^y=N，则log_aM=x，log_aN=y（a＞0，a≠1，M、N均为正数），
∵a^x•a^y=a^x+y，∴a^x+y=M•N∴log_aMN=x+y，即log_aMN=log_aM+log_aN
这是对数运算的重要性质之一，进一步，
我们还可以得出：log_aM₁M₂M₃…M_n=log_aM₁+log_aM₂+…+log_aM_n．（其中M₁、M₂、M₃、…、M_n均为正数，a＞0，a≠1）．
（3）请你猜想：${log}_{a}\frac{M}{N}$=log_aM-log_aN（a＞0，a≠1，M、N均为正数）．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

7．

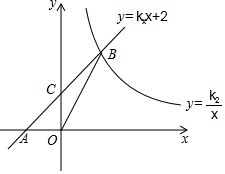如图，在平面直角坐标系中，一次函数y=k₁x+2的图象与x轴交于点A，与y轴交于点C，与反比例函数y=$\frac{{k}_{2}}{x}$的图象在第一象限内交于点B，连结BO．若S_△OBC=1，tan∠BOC=$\frac{1}{3}$．
（1）求一次函数与反比例函数的解析式；
（2）点P是反比例函数y=$\frac{{k}_{2}}{x}$（x＞0）图象上异于点B的另一点，若S_△PAO=5，求点P的坐标．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

14．计算：
（1）（-24）÷6×（-4）
（2）（-1）⁴-2×|-3|+$\root{3}{-64}$
（3）（-$\frac{2}{27}$+$\frac{2}{9}$-$\frac{1}{3}$）×（-27）
（4）90°36'-18.15°．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

11．计算：
（1）（-44）×（$\frac{1}{2}$-$\frac{1}{4}$×$\frac{5}{11}$）；
（2）（-2）³+5÷（-$\sqrt{\frac{25}{4}}$）

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

12．已知关于x的一元二次方程x²-2x+m=0有两个不相等的实数根，则m的取值范围是（　　）

A．

m＞1

B．