
【题目】已知等腰直角![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上一点,以
边上一点,以![]() 为边作等腰直角
为边作等腰直角![]() ,其中
,其中![]() ,边
,边![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 是
是![]() 上一点.
上一点.
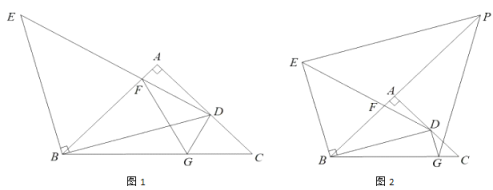
(1)如图1,若![]() ,连接
,连接![]() .
.
①若![]() ,求
,求![]() 的长度;
的长度;
②求证:![]() ;
;
(2)如图2,若![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,请猜想线段
,请猜想线段![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
【题目】某校举办园博会知识竞赛,打算购买A、B两种奖品.如果购买A奖品10件、B奖品5件,共需120元;如果购买A奖品5件、B奖品10件,共需90元.
(1)A,B两种奖品每件各多少元?
(2)若购买A、B奖品共100件,总费用不超过600元,则A奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践:
动手操作:如图1,四边形![]() 是一张矩形纸片,
是一张矩形纸片,![]() ,点
,点![]() 分别在
分别在![]() 边上,且
边上,且![]() ,连接
,连接![]() ,将
,将![]() 分别沿
分别沿![]() 折叠,点
折叠,点![]() 分别落在点
分别落在点![]() 处.
处.
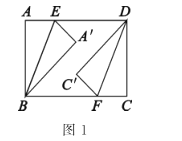
探究展示:(1)“刻苦小组”发现:![]() ,且
,且![]() ,并展示了如下的证明过程.
,并展示了如下的证明过程.
证明:在矩形![]() 中,
中,![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() (依据1)
(依据1)
∴![]() ,
,
∴![]() (依据2)
(依据2)
反思交流:①上述证明过程中的“依据1”与“依据2”分别指什么?
②“勤奋小组”认为:还可以通过证明四边形![]() 是平行四边形获证,请你根据“勤奋小组”的证明思路写出证明过程.
是平行四边形获证,请你根据“勤奋小组”的证明思路写出证明过程.
猜想证明:(2)如图2,折叠过程中,当点![]() 在直线
在直线![]() 的同侧时,延长
的同侧时,延长![]() 交
交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() 中,则四边形
中,则四边形![]() 是什么特殊四边形?请说明理由.
是什么特殊四边形?请说明理由.
联想拓广:(3)如图3,连接![]() ,
,
①当![]() 时,
时,![]() 的长为_____________________;
的长为_____________________;
②![]() 的长有最小值吗?若有,请你直接写出
的长有最小值吗?若有,请你直接写出![]() 的最小值;若没有,请说明理由.
的最小值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳某百果园店售卖赣南脐橙,已知每千克脐橙的成本价为![]() 元,在销售脐橙的这
元,在销售脐橙的这![]() 天时间内,销售单价
天时间内,销售单价![]() (元/千克)与时间第
(元/千克)与时间第![]() (天)之间的函数关系式为
(天)之间的函数关系式为![]() (
(![]() ,且
,且![]() 为整数),日销售量
为整数),日销售量![]() (千克)与时间第
(千克)与时间第![]() (天)之间的函数关系式为
(天)之间的函数关系式为![]() (
(![]() ,且
,且![]() 为整数)
为整数)
(1)请你直接写出日销售利润![]() (元)与时间第
(元)与时间第![]() (天)之间的函数关系式;
(天)之间的函数关系式;
(2)该店有多少天日销售利润不低于![]() 元?
元?
(3)在实际销售中,该店决定每销售![]() 千克脐橙,就捐赠
千克脐橙,就捐赠![]() 元给希望工程,在这
元给希望工程,在这![]() 天中,每天扣除捐赠后的日销售利润随时间
天中,每天扣除捐赠后的日销售利润随时间![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形![]() 内接于⊙
内接于⊙![]() ,
,![]() 是⊙
是⊙![]() 的直径,过点
的直径,过点![]() 的切线与
的切线与![]() 的延长线相交于点
的延长线相交于点![]() .且
.且![]() ,连接
,连接![]() .
.

(1)求证:![]() ;
;
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,当
,当![]() 时,求⊙
时,求⊙![]() 的半径;
的半径;
(3)在(2)的条件下,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
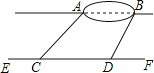
【题目】小明想测量湿地公园内某池塘两端A,B两点间的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=40°,再向前行走100米到点D处,测得∠BDF=52.44°,若直线AB与EF之间的距离为60米,求A,B两点的距离(结果精确到0.1)(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,sin52.44°≈0.79,cos52.44°≈0.61,tan52.44°≈1.30)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
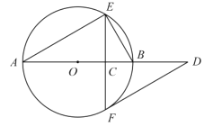
(1)已知![]() ,求
,求![]() 的大小(用含
的大小(用含![]() 的式子表示);
的式子表示);
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,请补全图形;若
,请补全图形;若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.假定每位顾客购买商品的可能性相同.
商品 顾客人数 | 甲 | 乙 | 丙 | 丁 |
100 | √ | × | √ | √ |
217 | × | √ | × | √ |
200 | √ | √ | √ | × |
300 | √ | × | √ | × |
85 | √ | × | × | × |
98 | × | √ | × | × |
(1)估计顾客同时购买乙和丙的概率为__________.
(2)如果顾客购买了甲,并且同时也在乙、丙、丁中进行了选购,则购买__________(填乙、丙、丁)商品的可能性最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com