
分析 根据题意可以画出相应的图形,根据锐角三角函数可以求得各个角的度数,从而可以求得各边的长度,本题得以解决.
解答 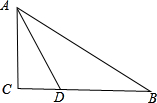 解:如右图所示,
解:如右图所示,
∵Rt△ABC中,∠C=90°,AC=15,∠A的平分线AD=10$\sqrt{3}$,
∴sin∠ADC=$\frac{AC}{AD}=\frac{15}{10\sqrt{3}}=\frac{\sqrt{3}}{2}$,
∴∠ADC=60°,
∴∠CAD=30°,
∴∠CAB=60°,∠B=30°,
∴AB=2AC=30,BC=15$\sqrt{3}$,
即∠CAB=60°,∠B=30°,BC=15$\sqrt{3}$,AB=30.
点评 本题考查解直角三角形,解题的关键是明确题意,利用锐角三角函数解答问题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 ①如图1,点A、C、B在同一直线上,CD平分∠ACB,∠ECF=90°.回答下列问题:
①如图1,点A、C、B在同一直线上,CD平分∠ACB,∠ECF=90°.回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价(元/件) | 100 | 110 | 120 | 130 | … |
| 月销量(件) | 200 | 180 | 160 | 140 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com