
分析 先求出不等式组的解集,求出不等式组的正整数解,代入后根据绝对值、偶次方的非负性得出6-z=0,3-y-m=0,求出即可.
解答 解:$\left\{\begin{array}{l}{3x<2x+2,①}\\{x-6≤0,②}\end{array}\right.$
∵解不等式①得:x<2,
解不等式①得:x≤6,
∴不等式组的解集为x<2,
∴不等式组的正整数解为1,
∵不等式组的正整数解满足|6x-z|+(3x-y-m)2=0,
∴|6-z|+(3-y-m)2=0,
∴6-z=0,3-y-m=0,
∴y=3-m,
∵y<0,
∴3-m<0,
∴m>3.
点评 本题考查了解一元一次不等式组,不等式组的整数解,绝对值、偶次方的非负性的应用,解此题的关键是能求出6-z=0和3-y-m=0,难度适中.


科目:初中数学 来源: 题型:选择题
| A. | m=-1,n=2.5 | B. | m=1,n=1.5 | C. | m=2,n=1 | D. | m=-2,n=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
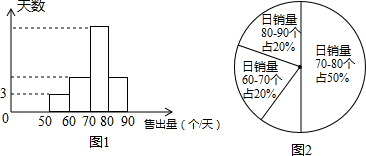
| 销售量/个 | 70 | 72 | 73 | 75 | 78 | 79 |
| 天数 | 1 | 2 | 3 | 4 | 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5件 | B. | 4件 | C. | 3件 | D. | 2件 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
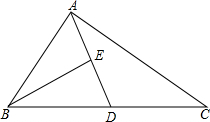 如图,AD为△ABC的中线,BE为△ABD的中线.
如图,AD为△ABC的中线,BE为△ABD的中线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com