
【题目】如图,要建一个长方形养鸡场,鸡场的一边靠墙,如果用50m长的篱笆围成中间有一道篱笆隔墙的养鸡场,设它的长度为x m.
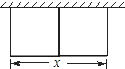
(1)要使鸡场面积最大,鸡场的长度应为多少m?
(2)如果中间有n(n是大于1的整数)道篱笆隔墙,要使鸡场面积最大,鸡场的长应为多少m?
比较(1)(2)的结果,你能得到什么结论?
【答案】(1)鸡场的长度为25m时,其面积最大为![]() m2;(2)无论鸡场中间有多少道篱笆隔墙,要使鸡场面积最大,其长都是25m.
m2;(2)无论鸡场中间有多少道篱笆隔墙,要使鸡场面积最大,其长都是25m.
【解析】
本题利用求矩形面积公式,确定函数关系式,然后根据函数的性质及自变量取值范围,求面积的最大值.
(1)依题意得
鸡场面积y=x![]() =
=![]()
∵y=﹣![]() x2+
x2+![]() x=
x=![]() (x2﹣50x)
(x2﹣50x)
=﹣![]() (x﹣25)2+
(x﹣25)2+![]()
∴当x=25时,y最大=![]()
即鸡场的长度为25m时,其面积最大为![]() m2
m2
(2)如中间有n道隔墙,则隔墙长为![]() m
m
∴y=![]() x=﹣
x=﹣![]() x2+
x2+![]() x
x
=﹣![]() (x2﹣50x)=﹣
(x2﹣50x)=﹣![]() (x﹣25)2+
(x﹣25)2+![]()
当x=25时,y最大=![]()
即鸡场的长度为25m时,鸡场面积为![]() m2
m2
结论:无论鸡场中间有多少道篱笆隔墙,要使鸡场面积最大,其长都是25m.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为![]() 且∠AFG=60°,GE=2BG,则折痕EF的长为( )
且∠AFG=60°,GE=2BG,则折痕EF的长为( )
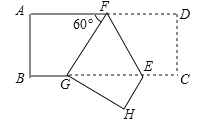
A. 1 B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
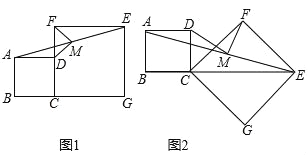
【题目】已知正方形ABCD和正方形CGEF,且D点在CF边上,M为AE中点,连接MD、MF,
(1)如图1,请直接给出线段MD、MF的数量及位置关系是 ;
(2)如图2,把正方形CGEF绕点C顺时针旋转,则(1)中的结论是否成立?若成立,请证明;若不成立,请给出你的结论并证明;
(3)若将正方形CGEF绕点C顺时针旋转30°时,CF边恰好平分线段AE,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
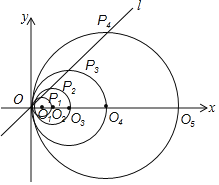
【题目】如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1,交x轴正半轴于点O2,以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4;…按此做法进行下去,其中![]() 的长为_____.
的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
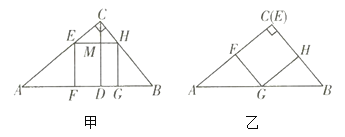
【题目】现有一块直角三角形的铁皮![]() ,
,![]() ,
,![]() ,
,![]() .要在其中剪出一个面积尽可能大的正方形,小红和小亮各想出了甲、乙两种方案,请你帮忙算一算哪一种方案剪出的正方形面积较大?
.要在其中剪出一个面积尽可能大的正方形,小红和小亮各想出了甲、乙两种方案,请你帮忙算一算哪一种方案剪出的正方形面积较大?
查看答案和解析>>
科目:初中数学 来源: 题型:
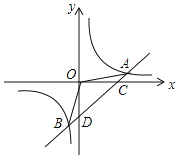
【题目】如图,一次函数y=kx+b(k≠0)和反比例函数y=![]() (m≠0)交于点A(4,1)与点B(﹣1,n).
(m≠0)交于点A(4,1)与点B(﹣1,n).
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等腰三角形,顶角∠BAC=![]() (
(![]() <600),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转
<600),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转![]() 到AE,过点E作BC的平行线,交AB于点F,连接DE、BE、DF
到AE,过点E作BC的平行线,交AB于点F,连接DE、BE、DF
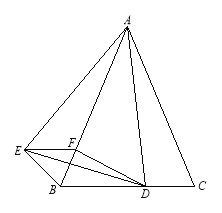
(1)求证:BE=CD
(2)若AD⊥BC,试判断四边形BDFE的形状,并给出证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低![]() 元.
元.
(1)填表:(不需化简)

(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
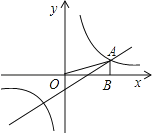
【题目】如图,反比例函数![]() 的图象经过点A(4,b),过点A作AB⊥x轴于点B,△AOB的面积为2.
的图象经过点A(4,b),过点A作AB⊥x轴于点B,△AOB的面积为2.
(1)求k和b的值;
(2)若一次函数y=ax﹣3的图象经过点A,求这个一次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com