
【题目】如图,四边形ABCD为正方形,E为对角线BD上的动点,过点E作FG⊥AE,FG交射线CD于F,交射线CB于G.
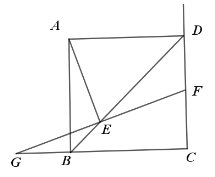
(1)求证:EF=EG
(2)求证:![]()
(3)若AB=4,当∠GEB=22.5°,直接写出CF的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)如下图,先证△ABE≌△CBE,得出∠1=∠3,再通过角度转化,得出∠2=∠3和∠4=∠5,从而得出EF=EC=EG;
(2)如下图,先得出△GEH∽△GFC,根据相似三角形的线段成比例可求证;
(3)存在2种情况,一种是点F在线段CD上,另一种是点F在射线CD上,且在点D的上方,分别利用相似三角形和勾股定理可求得.
(1)证明:连接CE
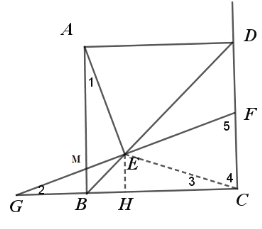
∵四边形ABCD为正方形
∴BA=BC,∠ABC=∠BCD=90°
∠ABE=∠CBE=45°
又∵BE=BE
∴△ABE≌△CBE(SAS)
∴∠1=∠3
又∵FG⊥AE
∴∠AEM=90°
∴∠1+∠AME=90°
又∵∠2+∠BMG=∠ABC=90° ∠AME=∠BMG
∴∠1=∠2
∴∠2=∠3
∴EG=EC
又∵∠3+∠4=90° ∠2+∠5=90°
∴∠4=∠5
∴EF=EC
∴EF=EG
(2)作EH⊥BC交BC于H
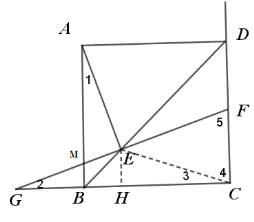
则∠GHE=90°=∠BCD
又∵∠2=∠2
∴△GEH∽△GFC
∴![]()
∴FC=2EH=2×![]()
(3)情况一:点F在线段CD上,图形如下
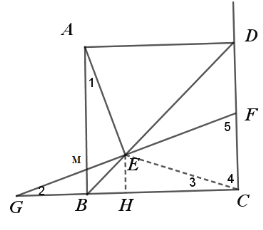
∵∠GEB=22.5°,BD是正方形ABCD的对角线
∴∠DBC=45°,∠BGE=22.5°
∴GB=BE
设BH=x,则HC=4-x
∴GB=HC-BH=4-2x=BE
∵CF=![]()
∴CF=![]()
∴EH=![]()
在Rt△EBH中,![]()
解得:x=4![]() 或x=4
或x=4![]() (舍)
(舍)
∴CF=8![]()
情况二:点F在射线CD上,且在点D的上方,图形如下,连接EC,过点E作EH⊥CD于点H
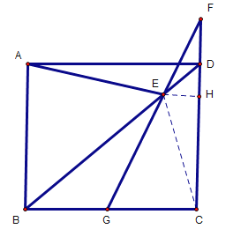
同理可得FC=![]()
综上得;CF=![]() .
.


科目:初中数学 来源: 题型:
【题目】2020年是决胜全面建成小康社会冲锋之年,为进一步加快脱贫攻坚步伐,某市出台了民生兜底、医保脱贫、教育救助、产业扶持、养老托管和易地搬迁这六种帮扶措施,每户贫困户都享受了2到5种帮扶措施,现把享受了2种、3种、4种和5种帮扶措施的贫困户分别称为A、B、C、D类贫困户.为检査帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成下面两幅不完整的统计图:
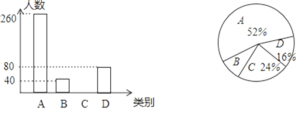
请根据图中信息回答下面的问题:
(1)求本次抽样调查贫困户总户数,并补全条形统计图;
(2)若该地共有15000户贫困户,请估计至少得到3项帮扶措施的大约有多少户;
(3)为更好地做好精准扶贫工作,现准备从D类贫困户中的甲、乙、丙、丁四户中随机选取两户进行重点帮扶,请用列表法或画树状图的方法,求出恰好选中甲和丙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的进步和网络资源的丰富,在线学习已经成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
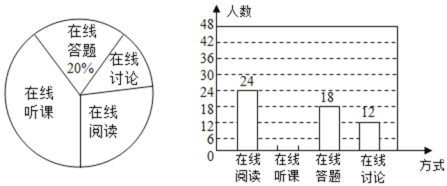
(1)求本次调查的学生总人数,并补全条形统计图;
(2)求扇形统计图中“在线讨论”对应的扇形圆心角的度数;
(3)该校共有学生3000人,请你估计该校对在线阅读最感兴趣的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
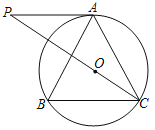
【题目】如图,△ABC内接于⊙O,AB=AC,过A作AP∥BC交CO的延长线于点P.
(1)求证:PA是⊙O的切线;
(2)若BC=8,tanB=2,求PA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(抗击疫情)为了遏制新型冠状病毒疫情的蔓延势头,各地教育部门在推迟各级学校开学时间的同时提出“听课不停学”的要求,各地学校也都开展了远程网络教学,某校集中为学生提供四类在线学习方式:在线阅读、在线听课、在线答疑、在线讨论,为了了解学生的需求,该校通过网络对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据结果绘制成如下两幅不完整的统计图。
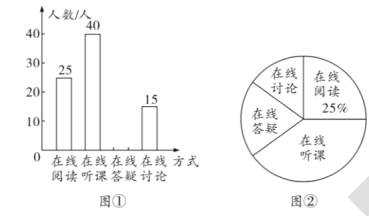
(1)本次调查的人数有多少人?
(2)请补全条形图;
(3)请求出“在线答疑”在扇形图中的圆心角度数;
(4)小宁和小娟都参加了远程网络教学活动,请求出小宁和小娟选择同一种学习方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(抗击疫情)为了遏制新型冠状病毒疫情的蔓延势头,各地教育部门在推迟各级学校开学时间的同时提出“听课不停学”的要求,各地学校也都开展了远程网络教学,某校集中为学生提供四类在线学习方式:在线阅读、在线听课、在线答疑、在线讨论,为了了解学生的需求,该校通过网络对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据结果绘制成如下两幅不完整的统计图。

(1)本次调查的人数有多少人?
(2)请补全条形图;
(3)请求出“在线答疑”在扇形图中的圆心角度数;
(4)小宁和小娟都参加了远程网络教学活动,请求出小宁和小娟选择同一种学习方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AC=2,AB=3,BC=4,点G是△ABC的重心.将△ABC平移,使得顶点A与点G重合.那么平移后的三角形与原三角形重叠部分的周长为( )
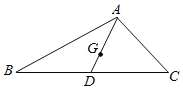
A.2B.3C.4D.4.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com