
【题目】如图,为加快城乡对接,建设全域美丽乡村,某地区对A,B两地间的公路进行改建.如图,A,B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米,∠A=45°,∠B=30°,开通隧道后,汽车从A地到B地大约可以少走多少千米(结果精确到1千米)?(参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)

【答案】汽车从A地到B地比原来少走为27千米.
【解析】
过点C作AB的垂线CD,垂足为D,在直角△ACD中,解直角三角形求出CD的长度和AC的长度,在直角△CBD中,解直角三角形求出BD的长度,再求出AD的长度,进而求出汽车从A地到B地比原来少走多少路程.
过点C作AB的垂线CD,垂足为D,
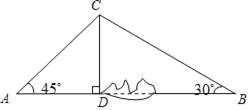
∵AB⊥CD,sin30°=![]() ,BC=80千米,
,BC=80千米,
∴CD=BCsin30°=80×![]() =40(千米),
=40(千米),
AC=![]() ≈56.4(千米),
≈56.4(千米),
∵cos30°=![]() ,BC=80(千米),
,BC=80(千米),
∴BD=BCcos30°=80×![]() =40
=40![]() (千米),
(千米),
∵tan45°=![]() ,CD=40(千米),
,CD=40(千米),
∴AD=40(千米),
∴AB=AD+BD=40+40![]() ≈40+40×1.73=109.2(千米),
≈40+40×1.73=109.2(千米),
∴汽车从A地到B地比原来少走多少路程为:AC+BC-AB=136.4-109.2=27.2≈27(千米).
答:汽车从A地到B地比原来少走的路程为27千米.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
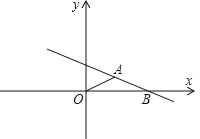
【题目】如图,在平面直角坐标系中,△ABO为底角是30°的等腰三角形,OA=AB=4,O为坐标原点,点B在x轴上,点P在直线AB上运动,当线段OP最短时,点P的坐标为( )
A. (1,1) B. (![]() ,3) C. (3,
,3) C. (3,![]() ) D. (2,2)
) D. (2,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
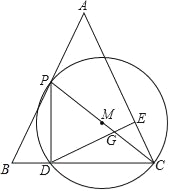
【题目】在△ABC中,AB=AC=2![]() ,BC=4,P是AB上一点,连接PC,以PC为直径作⊙M交BC于D,连接PD,作DE⊥AC于点E,交PC于点G,已知PD=PG,则BD=_____.
,BC=4,P是AB上一点,连接PC,以PC为直径作⊙M交BC于D,连接PD,作DE⊥AC于点E,交PC于点G,已知PD=PG,则BD=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于三角函数有如下公式:sin(α+β)=sinαcosβ+cosαsinβ,sin(α﹣β)=sinαcosβ﹣cosαsinβ;cos(α+β)=cosαcosβ﹣sinαsinβ,cos(α﹣β)=cosαcosβ+sinαsinβ;tan(α+β)=![]() (1﹣tanαtanβ≠0),合理利用这些公式可以将一些角的三角函数值转化为特殊角的三角函数来求值,如sin90°=sin(30°+60°)=sin30°cos60°+cos30°sin60°=
(1﹣tanαtanβ≠0),合理利用这些公式可以将一些角的三角函数值转化为特殊角的三角函数来求值,如sin90°=sin(30°+60°)=sin30°cos60°+cos30°sin60°=![]() =1,利用上述公式计算下列三角函数①sin105°=
=1,利用上述公式计算下列三角函数①sin105°=![]() ,②tan105°=﹣2﹣
,②tan105°=﹣2﹣![]() ,③sin15°=
,③sin15°=![]() ,④cos90°=0,其中正确的个数有( )
,④cos90°=0,其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
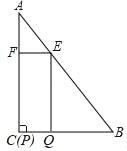
【题目】如图,在△ABC中,∠A=30°,∠C=90°,AB=12,四边形EFPQ是矩形,点P与点C重合,点Q、E、F分别在BC、AB、AC上(点E与点A、点B均不重合).
(1)当AE=8时,求EF的长;
(2)设AE=x,矩形EFPQ的面积为y.
①求y与x的函数关系式;
②当x为何值时,y有最大值,最大值是多少?
(3)当矩形EFPQ的面积最大时,将矩形EFPQ以每秒1个单位的速度沿射线CB匀速向右运动(当点P到达点B时停止运动),设运动时间为t秒,矩形EFPQ与△ABC重叠部分的面积为S,求S与t的函数关系式,并写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,∠ADC=60°,BD是一条对角线,点P在边CD上(与点C,D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,在BD上取一点H,使HQ=HD,连接HQ,AH,PH.
(1)依题意补全图1;
(2)判断AH与PH的数量关系及∠AHP的度数,并加以证明;
(3)若∠AHQ=141°,菱形ABCD的边长为1,请写出求DP长的思路.(可以不写出计算结果)
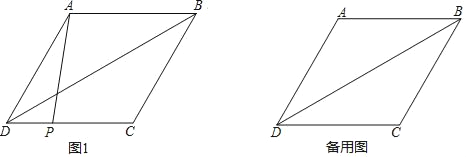
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列命题及函数y=﹣x,y=﹣x2,y=![]() 的图象.①如果﹣a>﹣
的图象.①如果﹣a>﹣![]() >﹣a2,那么a<﹣1;②如果﹣
>﹣a2,那么a<﹣1;②如果﹣![]() >﹣a2>﹣a,那么﹣1<a<0;③如果﹣a2>﹣a>﹣
>﹣a2>﹣a,那么﹣1<a<0;③如果﹣a2>﹣a>﹣![]() ,那么0<a<1;④如果﹣
,那么0<a<1;④如果﹣![]() >﹣a2>﹣a.那么a>1,则正确命题的序号是( )
>﹣a2>﹣a.那么a>1,则正确命题的序号是( )
A. ①② B. ②③ C. ①③ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=![]() +n(n<0)与坐标轴交于A、B两点,与y=
+n(n<0)与坐标轴交于A、B两点,与y=![]() (x>0)交于点E,过点E作EF⊥x轴,垂足为F,且△OAB∽△FEB,相似比为
(x>0)交于点E,过点E作EF⊥x轴,垂足为F,且△OAB∽△FEB,相似比为![]() .
.
(1)若n=-![]() ,求m的值;
,求m的值;
(2)连接OE,试探究m与n的数量关系,并直接写出直线OE的解析式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com