
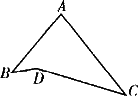
如图,已知∠BDC=150°,∠B=30°,∠C=40°,求∠A的度数.
|
解:方法一 如图甲,延长BD交AC于点E. ∵∠DEC=∠A+∠B(三角形的外角等于和它不相邻的两个内角的和) ∴∠A=∠DEC-∠B 同理∠DEC=∠BDC-∠C ∴∠A=∠BDC-∠C-∠B=150°-40°-30°=80° 方法二、方法三略. 分析:要求∠A的度数,应构造适当的三角形,让∠A成为该三角形的一个内角,然后利用三角形的内角和及其推论求之,此题可有如图甲、乙、丙三种辅助线作法.
注意:通过添辅助线构造三角形,将所求的角设定三角形的一内角或外角,利用三角形角之间的关系解题,是计算角的度数的常用方法,要熟练掌握,另外此题中有结论∠BDC=∠A+∠B+∠C |


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源:学习周报 数学 沪科八年级版 2009-2010学年 第11期 总167期 沪科版 题型:013
如图,已知∠BDC=128°,∠C=38°,∠B=23°,则∠A的度数为
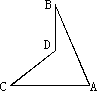
A.61°
B.60°
C.67°
D.39°
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江西省吉安市朝宗实验学校七年级下学期第一次段考数学试卷(带解析) 题型:解答题
如图,已知∠A=∠C,∠1+∠2=180°,试问:∠B与∠F有什么关系?为什么?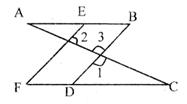
解:∠B=∠F,理由如下:
∵∠A=∠C
∴ ∥ ( )
∴∠BDC=∠B ( )
∵∠1+∠2=180°
且∠1+∠3 ( )
∴∠3+∠2=180°
∴ ∥ ( )
∴∠BDC= ( )
∴∠B=∠F ( )
查看答案和解析>>
科目:初中数学 来源:2015届江西省七年级下学期第一次段考数学试卷(解析版) 题型:解答题
如图,已知∠A=∠C,∠1+∠2=180°,试问:∠B与∠F有什么关系?为什么?

解:∠B=∠F,理由如下:
∵∠A=∠C
∴ ∥ ( )
∴∠BDC=∠B ( )
∵∠1+∠2=180°
且∠1+∠3 ( )
∴∠3+∠2=180°
∴ ∥ ( )
∴∠BDC= ( )
∴∠B=∠F ( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com