
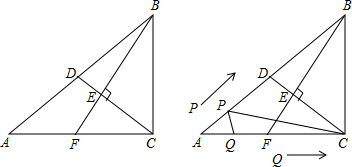
 ��ͼ��Rt��ABC�У���ACB=90�㣬BC=6��AC=8��D��б��AB���е㣬BF��CD�ڵ�E����AC�ڵ�F��
��ͼ��Rt��ABC�У���ACB=90�㣬BC=6��AC=8��D��б��AB���е㣬BF��CD�ڵ�E����AC�ڵ�F������ ��1������ֱ�������ε����ʵó���A=��ACD������ͬ�ǻ�Ƚǵ������ȵó���A=��CBF���Ӷ��ó�tan��CBF=tan��A=$\frac{3}{4}$���������CE��BE���ù��ɶ������BE��
��2���ٷֵ�Q���߶�AC��BC�ϣ��������ε������ʽ���������ϵʽ����ȷ����������ֵ��
�ڷ�������������ý�ƽ���߶������t��ֵ����CD��CQ��ʱ��t���ɣ�
��� �⣺��1����D��б��AB���е㣬
��CD=AD=$\frac{1}{2}$AB��
���A=��ACD��
�ߡ�ACD+��BCD=90�㣬
���A+��BCD=90�㣬
��BF��CD��
���BCD+��CBF=90�㣬
���A=��CBF��
��Rt��ABC��tan��A=$\frac{BC}{AC}=\frac{6}{8}$=$\frac{3}{4}$��
��tan��CBF=$\frac{3}{4}$��
��Rt��CBE����CE=3x��BE=4x��
���ݹ��ɶ����ã�CE2+BE2=BC2��
�ࣨ3x��2+��4x��2=36��
��x=-$\frac{6}{5}$���ᣩ��x=$\frac{6}{5}$��
��BE=4x=$\frac{24}{5}$��
��2������ͼ1�� ��
��
��0��t��8ʱ��
�ɣ�1��֪��tan��A=$\frac{3}{4}$��
��AP=t��AQ=t��
��PG=$\frac{3}{5}$t��CQ=8-t
��y=S��CPQ=$\frac{1}{2}$CQ��PG=$\frac{1}{2}$��8-t����$\frac{3}{5}t$=-$\frac{3}{10}��t-4��^{2}+\frac{24}{5}$��
��t=4ʱ��y���=$\frac{24}{5}$��
����ͼ2��
��8��t��10ʱ��
�ɣ�1��֪��tan��A=$\frac{3}{4}$��
��AP=t��AQ=t��
��AG=$\frac{4}{5}$t��CQ=t-8��
��PH=AG=8-$\frac{4}{5}$t��
��y=S��CPQ=$\frac{1}{2}$CQ��PH=$\frac{1}{2}$��t-8������8-$\frac{4}{5}$t��=-$\frac{2}{5}$��t-9��2+$\frac{2}{5}$��
��t=9ʱ��y���=$\frac{2}{5}$��
������t=4ʱ��y���=$\frac{24}{5}$��
��3������ʱ��t��ʹ��CPQ��CP�۵����Q�����߶�CD�ϣ�
����ͼ3������P���߶�AD�ϣ���Q��AC��ʱ������0��t��5��
�ɣ�1��֪��AQ=AP=t��
��DP=AD-AP=5-t��CQ=8-t
�ߡ�CPQ��CP�۵����Q�����߶�CD�ϣ�
���ACP=��DCP��
��$\frac{AC}{CD}=\frac{AP}{PD}$��DC��CQ��
��$\frac{8}{5}=\frac{t}{5-t}$��5��8-t��
��t=$\frac{40}{13}$��t��3
��t=$\frac{40}{13}$ʱ����CPQ��CP�۵����Q�����߶�CD�ϣ�
�ڵ���P���߶�DB�ϣ���Q��AC��ʱ������5��t��8��
��ʱ��P�͵�Q���߶�CD���࣬���ԡ�CPQ��CP�۵����Q�����������߶�CD�ϣ�
�۵���P���߶�DB�ϣ���Q���߶�CB��ʱ������8��t��10��
�ɣ�1��֪��AP=t��CQ=t-8��
��BP=10-t��DP=t-5��
�ߡ�CPQ��CP�۵����Q�����߶�CD�ϣ�
��$\frac{BC}{CD}=\frac{BP}{DP}$��CD��CQ��
��$\frac{6}{5}=\frac{10-t}{t-5}$��5��t-8��
��t=$\frac{80}{11}$��t��13��
��8��t��10��
��t=$\frac{80}{11}$��������������
������t=$\frac{40}{13}$ʱ����CPQ��CP�۵����Q�����߶�CD�ϣ�
���� �����Ǽ��α任�ۺ��⣬��Ҫ������ֱ�������ε����ʣ�������Ǻ����������ε������ʽ�����κ����ļ�ֵ��ȷ�����۵������ʣ���ƽ���߶������Ȿ��Ĺؼ��ǽ���������⣬�ѵ��Ƿ������ۣ�Ҫ����ȫ�棬��Ҫ©�⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
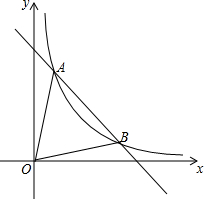 ��ͼ��һ�κ���y1=-x+5��ͼ���뷴��������y2=$\frac{k}{x}$��k��0���ڵ�һ����ͼ����A��1��n����B���㣮
��ͼ��һ�κ���y1=-x+5��ͼ���뷴��������y2=$\frac{k}{x}$��k��0���ڵ�һ����ͼ����A��1��n����B���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
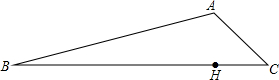
 ��ͼ������EFGH�ڽ��ڡ�ABC��AD��BC�ڵ�D����EH�ڵ�M����BC=8cm��AD=8cm��EH=3EF��EH=$\frac{72}{13}$cm��
��ͼ������EFGH�ڽ��ڡ�ABC��AD��BC�ڵ�D����EH�ڵ�M����BC=8cm��AD=8cm��EH=3EF��EH=$\frac{72}{13}$cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ͼ��ȡ�����ҹ��Ŵ���ѧ����ˬ�ġ�����Բ��ͼ����Ҳ�ơ���ˬ��ͼ�������������ĸ�ȫ�ȵ�ֱ�����������м��һ��С������ƴ�ɵ�һ���������Σ���ͼ��ʾ������������ε������13��С�����ε������1��ֱ�������ν϶̵�ֱ�DZ�Ϊa���ϳ���ֱ�DZ�Ϊb������a+b��2��ֵ��
��ͼ��ͼ��ȡ�����ҹ��Ŵ���ѧ����ˬ�ġ�����Բ��ͼ����Ҳ�ơ���ˬ��ͼ�������������ĸ�ȫ�ȵ�ֱ�����������м��һ��С������ƴ�ɵ�һ���������Σ���ͼ��ʾ������������ε������13��С�����ε������1��ֱ�������ν϶̵�ֱ�DZ�Ϊa���ϳ���ֱ�DZ�Ϊb������a+b��2��ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com