
【题目】某礼堂第一排有m个座位,后面每排比前一排多一个座位,则第20排有( )个座位.
A.m+21
B.m+20
C.m+19
D.m+18
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
(1)求证:AP=BQ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先画出了如图的四边形ABCD,并写出了如下不完整的已知和求证. 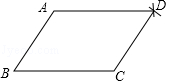
(1)在方框中填空,以补全已知和求证; 已知:如图,在四边形ABCD中,BC=AD, .
求证:四边形ABCD是 .
(2)写出证明过程:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料并解答问题:
关于勾股定理的研究有一个很重要的内容是勾股数组,在数学课本中我们已经了解到,“能够成为直角三角形三条边的三个正整数称为勾股数”,以下是毕达哥拉斯等学派研究出的确定勾股数组的两种方法:
方法1:若m为奇数(m≥3),则a=m,b=![]() (m2﹣1)和c=
(m2﹣1)和c=![]() (m2+1)是勾股数.
(m2+1)是勾股数.
方法2:若任取两个正整数m和n(m>n),则a=m2﹣n2,b=2mn,c=m2+n2是勾股数.
(1)在以上两种方法中任选一种,证明以a,b,c为边长的△ABC是直角三角形;
(2)某园林管理处要在一块绿地上植树,使之构成如下图所示的图案景观,该图案由四个全等的直角三角形组成,要求每个三角形顶点处都植一棵树,各边上相邻两棵树之间的距离均为1米,如果每个三角形最短边上都植6棵树,且每个三角形的各边长之比为5:12:13,那么这四个直角三角形的边长共需植树 棵.
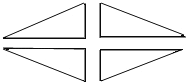
(3)某家俱市场现有大批如图所示的梯形边角余料(单位:cm),实验初中数学兴趣小组决定将其加工成等腰三角形,且方案如下:
三角形中至少有一边长为10 cm;三角形中至少有一边上的高为8 cm,
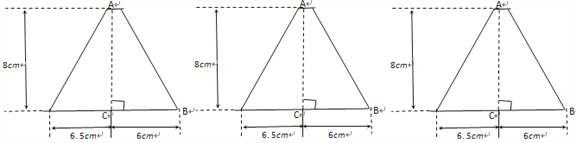
请设计出三种面积不同的方案并在图上画出分割线,求出相应图形面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程 x2﹣4x﹣7=0 时,需要将原方程化为( )
A. (x + 2)2 =11B. (x+2)2= 7
C. (x﹣2)2 =11D. (x﹣2)2= 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏从A地出发向B地行走,同时小聪从B地出发向A地行走,如图所示,相交于点P的两条线段l1、l2分别表示小敏、小聪离B地的距离y(km)与已用时间x(h)之间的关系,则小敏、小聪行走的速度分别是( )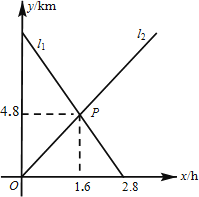
A.3km/h和4km/h
B.3km/h和3km/h
C.4km/h和4km/h
D.4km/h和3km/h
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com