
����Ŀ����������ͼ�����д������ε�����ɱ�ʾΪ��a+b��2 �� Ҳ�ɱ�ʾΪc3+4��![]() ab��������a+b��2=c2+4��
ab��������a+b��2=c2+4��![]() ab���ɴ��Ƶ���һ����Ҫ�Ľ���a2+b2=c2 �� �����Ҫ�Ľ��۾��������ġ����ɶ����������ָ���ͼ�ο��Լ���ֱ�����ۻ���֤��ѧ���ɺ�ʽ�ķ�������ơ�����֤������
ab���ɴ��Ƶ���һ����Ҫ�Ľ���a2+b2=c2 �� �����Ҫ�Ľ��۾��������ġ����ɶ����������ָ���ͼ�ο��Լ���ֱ�����ۻ���֤��ѧ���ɺ�ʽ�ķ�������ơ�����֤������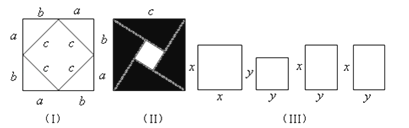
��1��������ͼ����2002�������ѧ�Ҵ���꣩���������ʽ��֤���ɶ����������ĸ�ֱ�������εĽϴ��ֱ�DZ߳���Ϊa����С��ֱ�DZ߳���Ϊb��б�߳���Ϊc����
��2�������ã����ṩ��ͼ�ν�����ϣ������ͼ�ε��������ʽ��֤����x+2y��2=x2+4xy+4y2 ��
���𰸡��⣺��1��S��Ӱ=4��![]() ab��S��Ӱ=c2����a��b��2 ��
ab��S��Ӱ=c2����a��b��2 ��
��4��![]() ab=c2����a��b��2 �� ��2ab=c2��a2+2ab��b2 ��
ab=c2����a��b��2 �� ��2ab=c2��a2+2ab��b2 ��
��a2+b2=c2��
��2����ͼ��ʾ��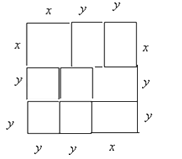
�������ε����Ϊx2+4y2+4xy��Ҳ����Ϊ��x+2y��2 ��
��x+2y��2=x2+4xy+4y2 ��
����������1����Ӱ��������ɴ������������ȥС�����������Ҳ�������ĸ�ֱ�����������֮�������������ȼ��ɵ�֤��
��2��ƴ����ͼ��ʾͼ�Σ����ݴ������α߳�Ϊx+2y����ʾ���������������������С�������������������֮�������������֤��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�����������ε����߳���3cm��7cm���������ܳ�Ϊ��������
A. 13cm B. 17cm C. 13��17cm D. 10cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
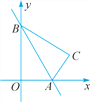
����Ŀ����ͼ�� һ�κ�����ͼ����x����y��ֱ��ཻ�ڵ�A��B������AOB��ֱ��AB����������ACB.����C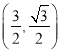 �����һ�κ����ı���ʽ��
�����һ�κ����ı���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������ʵ���У��ס�����������ȼ��ʱʣ�ಿ�ֵĸ߶�![]() ��cm����ȼ��ʱ��
��cm����ȼ��ʱ��![]() ��h���Ĺ�ϵ��ͼ��ʾ. �����ͼ�����ṩ����Ϣ������и����⣺
��h���Ĺ�ϵ��ͼ��ʾ. �����ͼ�����ṩ����Ϣ������и����⣺

��1��������������ȼ��ǰ�ĸ߶ȷֱ��� ���ӵ�ȼ��ȼ�����õ�ʱ��ֱ��� ��
��2���ֱ�����ס�����������ȼ��ʱ![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��3����![]() Ϊ��ֵʱ���ס�������������ȼ�յĹ����еĸ߶���ȣ�
Ϊ��ֵʱ���ס�������������ȼ�յĹ����еĸ߶���ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪BE��CF�ֱ�����ABC��AC��AB���ϵĸ�������BE���ӳ�����ȡ��P��ʹPB��AC����CF���ӳ�����ȡ��Q��ʹCQ��AB.��֤��AQ��AP.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A�������ǣ�4����3��������A����x��ĶԳƵ㣬�õ���A����������A������y��ĶԳƵ㣬�õ���A�������A����������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������й����ͨ�����У��滮��A��B������һ�ε�������B�ڵ�A��������������A��B֮�佨����϶࣬��ֱ�Ӳ������ֲ�ù���C�ڵ�A�ı�ƫ��45�㷽���ϣ��ڵ�B�ı�ƫ��60�㷽���ϣ�BC=400m�����������ε���AB�ij��ȣ��������ȷ��1m���ο����ݣ�![]() ��
��![]() ��
��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��ѧ����ֽ�ʲ��ԡ�ʵ���������ɳ���¼����ɼ��ֱ�50%��20%��30%�ı�������ѧ�������ɼ���90������Ϊ���㣮�ס��ҡ������˵ĸ���ɼ����±�����λ���֣���ѧ�������ɼ�������ǣ� ��
ֽ�ʲ��� | ʵ������ | �ɳ���¼ | |
�� | 90 | 83 | 95 |
�� | 88 | 90 | 95 |
�� | 90 | 88 | 90 |
A. �� B. �ҡ��� C. �ס��� D. �ס���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����в���ʽ������ȷ���ǣ�������
A.��a��b����a��2��b��2
B.��-![]() ?a<2����a����4
?a<2����a����4
C.��a��b����1��2a��1��2b
D.��a��b����ac2��bc2
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com