
分析 (1)观察一系列等式得到一般性规律,写出即可;
(2)原式右边利用平方差公式化简,计算得到结果与左边相等,即可得证.
解答 解:(1)m•n=($\frac{m+n}{2}$)2-($\frac{m-n}{2}$)2;
(2)∵右边=($\frac{m+n}{2}$+$\frac{m-n}{2}$)($\frac{m+n}{2}$-$\frac{m-n}{2}$)=mn=左边,?
∴m•n=($\frac{m+n}{2}$)2-($\frac{m-n}{2}$)2.
故答案为:(1)m•n=($\frac{m+n}{2}$)2-($\frac{m-n}{2}$)2
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
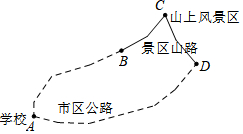 为了提倡“原色青春,绿色行走!”,某市某校组织学生从学校(点A)出发,沿A→B→C→D→A的路线参加总路程为14km绿色行走活动,其中路线A→B段、D→A段是我市区公路,B→C段、C→D段是景区山路.已知学生队伍在市区公路的行进速度为6km/h,在景区山路的行进速度为2km/h,本次行走共用3.5h.问本次行走活动中市区公路、景区山路各多少km?
为了提倡“原色青春,绿色行走!”,某市某校组织学生从学校(点A)出发,沿A→B→C→D→A的路线参加总路程为14km绿色行走活动,其中路线A→B段、D→A段是我市区公路,B→C段、C→D段是景区山路.已知学生队伍在市区公路的行进速度为6km/h,在景区山路的行进速度为2km/h,本次行走共用3.5h.问本次行走活动中市区公路、景区山路各多少km?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
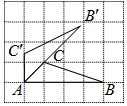 如图,△ABC的三个顶点都在正方形网格的格点处,若将△ABC绕点A逆时针旋转得到△A′B′C′,则tanB′的值为( )
如图,△ABC的三个顶点都在正方形网格的格点处,若将△ABC绕点A逆时针旋转得到△A′B′C′,则tanB′的值为( )| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{\sqrt{10}}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com