
����Ŀ������ƽ��ֱ������ϵxOy�еĵ�P�͡�C���������¶��壺�����C�İ뾶Ϊr����C��һ��P����C�����߳�С�ڻ����2r����ô��P������C�������ĵ���.
��1������O�İ뾶Ϊ1ʱ��
���ڵ�P1��![]() ��
�� ![]() ����P2��0����2����P3��
����P2��0����2����P3��![]() ��0���У���O�������ĵ����� ��
��0���У���O�������ĵ����� ��
�ڵ�P��m��n����ֱ��![]() �ϣ��ҵ�P�ǡ�O�������ĵ��������P������m��ȡֵ��Χ��
�ϣ��ҵ�P�ǡ�O�������ĵ��������P������m��ȡֵ��Χ��
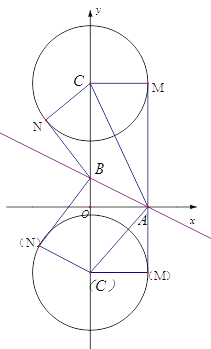
��2����C��Բ��C��y���ϣ��뾶Ϊ2��ֱ��![]() ��x�ᡢy��ֱ��ڵ�A��B. ����߶�AB�ϵ����е㶼�ǡ�C�������ĵ�������ֱ��д��Բ��C�������ȡֵ��Χ.
��x�ᡢy��ֱ��ڵ�A��B. ����߶�AB�ϵ����е㶼�ǡ�C�������ĵ�������ֱ��д��Բ��C�������ȡֵ��Χ.
���𰸡���1����![]() ��
�� ![]() ����1��m��2����2��Բ��C������
����1��m��2����2��Բ��C������![]() ��ȡֵ��ΧΪ��
��ȡֵ��ΧΪ�� ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
�������������������1����������㵽��O�����߳�������¶�������жϼ��ɵã�
���ú�m�Ĵ���ʽ��ʾ����P����O�����߳�������¶�����бȽϺ�õ�����m�IJ���ʽ�������ɵã�
��2�������A��B�������꣬��C����Ϊ��0��yC ����AM��BN�ֱ�Ϊ��C�����ߣ��е�ֱ�ΪM��N������AM2=![]() ��BN2 =
��BN2 =![]() �����߶�AB�ϵ����е㶼�ǡ�C�ġ����ĵ㡱���ò���ʽ��
�����߶�AB�ϵ����е㶼�ǡ�C�ġ����ĵ㡱���ò���ʽ��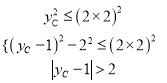 ���ⲻ��ʽ�鼴�ɵ�..
���ⲻ��ʽ�鼴�ɵ�..
�����������1���ٹ���P2����O������P2N���е�ΪN������P3����O������P3M���е�ΪM��
���P2NO=��P3MO=90�㣬
��P2N=![]() =
=![]() ��
��
P3M=![]() =2��
=2��
�ߡ�O�İ뾶r=1�����P2��P3�ǡ�O�������ĵ�����
��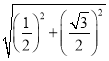 =1������P1��
=1������P1��![]() ��
�� ![]() ������O�ϣ����P1��
������O�ϣ����P1��![]() ��
�� ![]() ����ʾ��O�������ĵ�����
����ʾ��O�������ĵ�����
�ʴ�Ϊ�� ![]() ��
�� ![]() ��
��
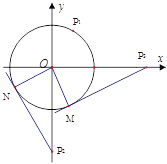
�ڹ���P���ѵ�����PM���е�ΪM��
��P��m����m��3������PM2=PO2-OM2=m2+(-m+3)2-12=2m2-6m+8��
�ߵ�P�ǡ�O�������ĵ�������O�İ뾶Ϊ1��
��PM��2��
��2m2-6m+8�ܣ�2��1��2��
��1��m��2��
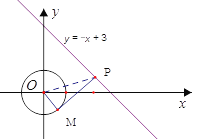
��2��ֱ��![]() ��x�ᡢy��ֱ��ڵ�A��B������A��2��0����B��0��1����
��x�ᡢy��ֱ��ڵ�A��B������A��2��0����B��0��1����
��C����Ϊ��0��yC ����AM��BN�ֱ�Ϊ��C�����ߣ��е�ֱ�ΪM��N��
��ͼ��AM2=AC2-CM2=![]() =
=![]() ��
��
BN2=BC2-CN2=![]() ��
��
���߶�AB�ϵ����е㶼�ǡ�C�ġ����ĵ㡱��
��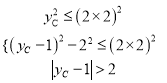 ��
��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��Բ��C������![]() ��ȡֵ��ΧΪ��
��ȡֵ��ΧΪ�� ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ����B��x���ϣ���
����B��x���ϣ���![]() ��
��
![]() ���B�����ꣻ
���B�����ꣻ
![]() ��
��![]() �������
�������
![]() ��y�����Ƿ����P��ʹ��A��B��P����Ϊ����������ε����Ϊ10�������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
��y�����Ƿ����P��ʹ��A��B��P����Ϊ����������ε����Ϊ10�������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����ǰ尴��ͼ��ʾ�ķ�ʽ�ڷţ����С�ABCΪ����45��ǵ����ǰ壬ֱ��AD�ǵ���ֱ�����ǰ�ĶԳ��ᣬ��б���ϵĵ�DΪ��һ�����ǰ�DMN��ֱ�Ƕ��㣬DM��DN�ֱ�AB��AC�ڵ�E��F���������ĸ����ۣ���BD��AD��CD���ڡ�AED�ա�CFD����BE+CF��EF����S�ı���AEDF��![]() BC2��������ȷ������_____������ţ���
BC2��������ȷ������_____������ţ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڱ����п�չ�����������ȷ������У�ij��ѧС�鵽����Ӣ�ۼ��վ��ִ�ڣ����ڻ��ʵ�ز����˼���ĸ߶�. �������£���ͼ�������ڲ�����A���ø�Ϊ1.5m�IJ����AC�������Ӣ�ۼ��MN����M������Ϊ35����Ȼ���ڲ�����B����ͬ���IJ����BD�������Ӣ�ۼ��MN����M������Ϊ45������������A��B�����ľ���Ϊ15m������N��B��A������һ��ֱ���ϣ�����CD���ӳ���MN�ڵ�E. �����������ǵIJ����������������Ӣ�ۼ��MN�ĸ߶�.
���ο����ݣ�sin35���0.6��cos35���0.8��tan35���0.7��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʽ��2x��1����x+3����0�Ľ⼯��
�⣺���ݡ�ͬ��������ˣ���Ϊ�����ɵã���![]() �� ��
�� ��![]() ��
��
��ٵ�x��![]() ����ڵ�x����3��
����ڵ�x����3��
���ʽ�Ľ⼯Ϊx��![]() ��x����3��
��x����3��
�������������������������⣺
��1����ʽ��2x��3����x+1����0�Ľ⼯��
��2����ʽ![]() ��0�Ľ⼯��
��0�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P��![]() ����������ʾ�����˶���ÿ������������OABC�ı�ʱ����з���������ʱ����ǵ�������ǣ�����P��2018�����������εı�ʱ����P������Ϊ______��
����������ʾ�����˶���ÿ������������OABC�ı�ʱ����з���������ʱ����ǵ�������ǣ�����P��2018�����������εı�ʱ����P������Ϊ______��

���𰸡�![]()
��������
���ݷ����������ǵĶ�������ͼ�Σ���ͼ��֪��ÿ6�η���Ϊһ��ѭ��������ѭ������2018����6�������̺����������ȷ������Ӧ�ĵ�����꼴�ɣ�
�⣺��ͼ��ʾ������6�η�����ص�������![]() ��
��
![]() ��
��
![]() ����P��2018���������εı�ʱΪ��337��ѭ����ĵ�2�η�����
����P��2018���������εı�ʱΪ��337��ѭ����ĵ�2�η�����
![]() ��P������Ϊ
��P������Ϊ![]() ��
��
�ʴ�Ϊ��![]() ��
��
���㾦��
������Ҫ�����˵������Ĺ��ɣ�����ͼ�Σ��۲��ÿ6�η���Ϊһ��ѭ��������ѭ���ǽ���Ĺؼ���
�����͡������
��������
15
����Ŀ��Ϊ�˱���������ij������˾��������A��B�����ͺŵ�ȫ�»�϶�����������10��������A���ͺ�ÿ���۸�Ϊa��Ԫ��ÿ���ʡ����Ϊ![]() ������B���ͺ�ÿ���۸�Ϊb��Ԫ��ÿ���ʡ����Ϊ
������B���ͺ�ÿ���۸�Ϊb��Ԫ��ÿ���ʡ����Ϊ![]() �����������飬����һ��A�ͳ��ȹ���һ��B�ͳ���20��Ԫ������2��A�ͳ��ȹ���3��B�ͳ���60��Ԫ��
�����������飬����һ��A�ͳ��ȹ���һ��B�ͳ���20��Ԫ������2��A�ͳ��ȹ���3��B�ͳ���60��Ԫ��
![]() �����a��b��
�����a��b��
![]() ������������϶���������ÿ���ܽ�ʡ
������������϶���������ÿ���ܽ�ʡ![]() �������ͣ�����������϶�����������Ҫ������Ԫ��
�������ͣ�����������϶�����������Ҫ������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��20��ײˣ���ÿ��18ǧ��Ϊ�������������ǧ�����ֱ���������������ʾ����¼���£�
��������IJ�ֵ����λ��ǧ�ˣ� |
|
|
| 0 | 1 | 2.5 |
���� | 2 | 3 | 2 | 1 | 4 | 8 |
��1��20��ײ��У����ص�һ��������һ���� ǧ�ˣ�
��2����������Ƚϣ�20��ײ��ܼƳ����������ǧ�ˣ�
��3�����ײ�ÿǧ���ۼ�1.3Ԫ���������20��ײ˿�������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�������Ϊ![]() Ԫ�M���������
Ԫ�M���������![]() Ԫ�M���ļ۸����ʱ��ÿ����۳�
Ԫ�M���ļ۸����ʱ��ÿ����۳�![]() ���������鵱����ÿ��
���������鵱����ÿ��![]() Ԫʱ��ÿ�����۳�
Ԫʱ��ÿ�����۳�![]() �������̳���ÿ����
�������̳���ÿ����![]() Ԫ������ÿ�����Ӧ�Ƕ���Ԫ������ÿ�������
Ԫ������ÿ�����Ӧ�Ƕ���Ԫ������ÿ�������![]() Ԫ��������˵����������� ��
Ԫ��������˵����������� ��
A. �Ǽۺ�ÿ����ߵ��ۼ���![]() Ԫ
Ԫ
B. �Ǽۺ�ÿ�����۳���ߵ�������![]() ��
��
C. �Ǽۺ�ÿ��������ߵ�������![]() ��
��
D. ���з���Ϊ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�![]() ��
��![]() ��
��![]() ��
��![]() ����һ����Ϊ2016����λ������û�е��Ե�ϸ��
����һ����Ϊ2016����λ������û�е��Ե�ϸ��![]() �ߵĴ�ϸ���Բ���
�ߵĴ�ϸ���Բ���![]() ��һ�˹̶��ڵ�A��������
��һ�˹̶��ڵ�A��������![]() �Ĺ��������ı���ABCD�ı��ϣ���ϸ����һ������λ�õĵ��������
�Ĺ��������ı���ABCD�ı��ϣ���ϸ����һ������λ�õĵ��������![]() ����
����![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com