
【题目】问题发现:
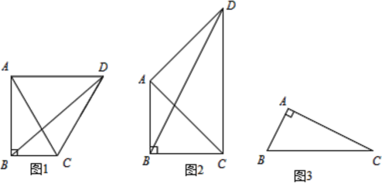
(1)如图1,在Rt△ABC中,∠BAC=30°,∠ABC=90°,将线段AC绕点A逆时针旋转,旋转角α=2∠BAC, ∠BCD的度数是 ;线段BD,AC之间的数量关系是 .
类比探究:
(2)在Rt△ABC中,∠BAC=45°,∠ABC=90°,将线段AC绕点A逆时针旋转,旋转角α=2∠BAC,请问(1)中的结论还成立吗?;
拓展延伸:
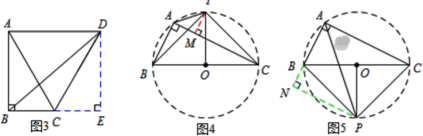
(3)如图3,在Rt△ABC中,AB=2,AC=4,∠BDC=90°,若点P满足PB=PC,∠BPC=90°,请直接写出线段AP的长度.
【答案】(1)120°,BD=![]() AC;(2)不成立,理由详见解析;(3)
AC;(2)不成立,理由详见解析;(3)![]() 或
或![]() .
.
【解析】
(1)过点D作DE⊥BC,通过线段之间的转换得到AC与DE之间的关系,在直角三角形BDE中通过BD与DE的关系,得到BD,AC之间的关系.
(2)类比(1)的解法,找线段之间的关系.
(3)分情况进行讨论,画出符合题意得图形进行求解.
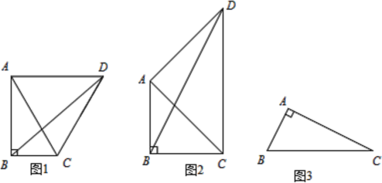
解:(1)如图3,过点D作DE⊥BC,垂足为E,设BC=m.
在Rt△ABC中,∠BAC=30°,由BC=AB·tan30°,BC=AC·sin30°,得AC=2m,BC=![]() m,
m,
∵AC=AD,∠CAD=2×30°=60°,∴△ACD为等边三角形,∴∠ACD=60°,CD=AC=2m,
∴∠BCD=60°×2=120°,在Rt△DEC中,∠DCE=180°-120°=60°,DC=2m,∴CE=CD·cos60°=m,DE=CE·tan60°=![]() m,∴在Rt△BED中,BD=
m,∴在Rt△BED中,BD=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,故BD=
,故BD=![]() AC.故答案为:120°;BD=
AC.故答案为:120°;BD=![]() AC.
AC.
(2)不成立,理由如下:
设BC=n,在Rt△ABC中,∠BAC=45°,∠ABC=90°,∴BC=AB=m,AC=![]() BC=
BC=![]() n,
n,
∵AC=AD,∠CAD=90°,∴△CAD为等腰直角三角形,∴∠ACD=45°,CD=![]() AC= 2n,
AC= 2n,
∴∠BCD=2×45°=90°,在Rt△BCD中,BD=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,,故BD=
,,故BD=![]() AC.答案为:90°;BD=
AC.答案为:90°;BD=![]() AC.故结论不成立.
AC.故结论不成立.
(3)AP的长为![]() 或
或![]() .;解答如下:
.;解答如下:
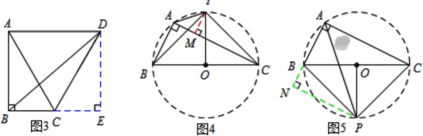
∵PB=PC,∴点P在线段BC的垂直平分线上,∵∠BAC=∠BCP=90°,故A、B、C、P四点共圆,以线段BC的中点为圆心构造⊙O,如图4,图5,分类讨论如下:
①当点P在直线BC上方时,如图4,作PM⊥AC,垂足为M,设PM=x.

∵PB=PC,∠BPC=90°,∴△PBC为等腰直角三角形,∴∠PBC=45°,
∵∠PAC=∠PBC=45°,∴△AMP为等腰直角三角形,∴AM=PM=x,AP=![]() PM=
PM=![]() x,
x,
在Rt△ABC中,AB=2,AC=4,∴BC=![]() =
=![]() ,∴PC=BC·sin45°=
,∴PC=BC·sin45°=![]() ,
,
在Rt△PMC中,∵∠PMC=90°,PM=x,PC=![]() ,CM=4-x,∴
,CM=4-x,∴![]() ,
,
解得:![]() ,
,![]() (舍),∴AP=
(舍),∴AP=![]() =
=![]() ;
;
②当点P在直线BC的下方时,如图5,作PN⊥AB的延长线,垂足为N,设PN=y.
同上可得PB=![]() ,△PAN为等腰三角形,∴AN=PN=y,∴BN=y-2,
,△PAN为等腰三角形,∴AN=PN=y,∴BN=y-2,
在Rt△PNB中,∵∠PNB=90°,PN=y,BN=y-2,PB=![]() ,∴
,∴![]() ,
,
解得:![]() ,
,![]() (舍),∴AP=
(舍),∴AP=![]() =
=![]() .故AP的长度为:
.故AP的长度为:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】(满分7分)五月石榴红,枝头鸟儿歌.一只小鸟从石榴树上的A处沿直线飞到对面一房屋的顶部C处.从A处看房屋顶部C处的仰角为![]() ,看房屋底部D处的俯角为
,看房屋底部D处的俯角为![]() ,石榴树与该房屋之间的水平距离为
,石榴树与该房屋之间的水平距离为![]() 米,求出小鸟飞行的距离AC和房屋的高度CD.
米,求出小鸟飞行的距离AC和房屋的高度CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳天虹某商场从厂家批发电视机进行零售,批发价格与零售价格如下表:
电视机型号 | 甲 | 乙 |
批发价(元/台) | 1500 | 2500 |
零售价(元/台) | 2025 | 3640 |
若商场购进甲、乙两种型号的电视机共50台,用去9万元.
(1)求商场购进甲、乙型号的电视机各多少台?
(2)迎“元旦”商场决定进行优惠促销:以零售价的七五折销售乙种型号电视机,两种电视机销售完毕,商场共获利8.5%,求甲种型号电视机打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】复课返校后,为了拉大学生锻炼的间距,学校决定增购适合独立训练的两种体育器材:跳绳和毽子.如果购进5根跳绳和6个毽子共需196元;购进2根跳绳和5个键子共需120元.
(1)求一根跳绳和一个毽子的售价分别是多少元;
(2)学校计划购买跳绳和键子两种器材共400个,由于受疫情影响,商场决定对这两种器材打折销售,其中跳绳以八折出售,毽子以七五折出售,学校要求跳绳的数量不少于毽子数量的3倍,跳绳的数量不多于310根,请你求出学校花钱最少的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
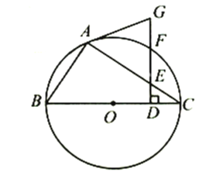
【题目】如图,![]() 为⊙
为⊙![]() 的内接三角形,
的内接三角形,![]() 为⊙
为⊙![]() 的直径,在线段
的直径,在线段![]() 上取点
上取点![]() (不与端点重合),作
(不与端点重合),作![]() ,分别交
,分别交![]() 、圆周于
、圆周于![]() 、
、![]() ,连接
,连接![]() ,已知
,已知![]() .
.
(1)求证:![]() 为⊙
为⊙![]() 的切线;
的切线;
(2)已知![]() ,填空:
,填空:
①当![]() __________
__________![]() 时,四边形
时,四边形![]() 是菱形;
是菱形;
②若![]() ,当
,当![]() __________时,
__________时,![]() 为等腰直角三角形.
为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自2020年初新冠肺炎疫情爆发以来,国内经济--度被按下暂停键,如今随着国内疫情防控形势持续向好,各地开始进人积极复工复产的新模式.某商家为降低疫情带来的影响,刺激消费,吸引顾客,特此设计了一个游戏,其规则是:分别转动如图所示的两个可以自由转动的转盘各一次,每次指针落在每一字母区域的机会均等(若指针恰好落在分界线上则重转),当两个转盘的指针所指字母相同时,消费者就可以获得一次八折优惠价购买商品的机会.
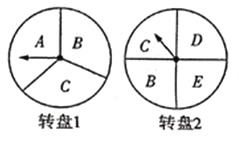
(1)用树状图或列表的方法表示出游戏可能出现的所有结果;
(2)若小亮参加一次游戏,则他能获得八折优惠价购买商品的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商店购进了足球和排球共20个,一共花了1360元,进价和售价如表:
足球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
(l)购进足球和排球各多少个?
(2)全部销售完后商店共获利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售A、B两种型号的电风扇,进价及售价如表:
品牌 | A | B |
进价(元/台) | 120 | 180 |
售价(元/台) | 150 | 240 |
(1)该商场4月份用21000元购进A、B两种型号的电风扇,全部售完后获利6000元,求商场4月份购进A、B两种型号电风扇的数量;
(2)该商场5月份计划用不超过42000元购进A、B两种型号电风扇共300台,且B种型号的电风扇不少于50台;销售时准备A种型号的电风扇价格不变,B种型号的电风扇打9折销售.那么商场如何进货才能使利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=a,∠ABC=60°,过点A作AE⊥BC,垂足为E,AF⊥CD,垂足为F.
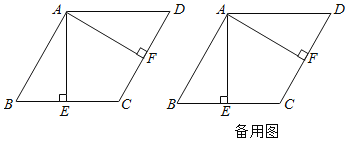
(1)连接EF,用等式表示线段EF与EC的数量关系,并说明理由;
(2)连接BF,过点A作AK⊥BF,垂足为K,求BK的长(用含a的代数式表示);
(3)延长线段CB到G,延长线段DC到H,且BG=CH,连接AG、GH、AH.
①判断△AGH的形状,并说明理由;
②若a=2,S△ADH=![]() (3+
(3+![]() ),求sin∠GAB的值.
),求sin∠GAB的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com