
【题目】同学们都知道:|5|在数轴上表示数5的点与原点的距离,而|5-(-2)|表示5与-2之差的绝对值,实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离.请你借助数轴进行以下探索:
![]()
(1)则![]() 表示 的距离.
表示 的距离.
(2)数轴上表示x与 7的两点之间的距离可以表示为 .
(3)如果|x-2|=5,则x= .
(4)同理|x+1|+|x-2|表示数轴上有理数x所对应的点到-1和2所对应的点的距离之和,请你找出所有符合条件的整数x,使得|x+1|+|x-2|=3,这样的整数是 .
(5)由以上探索猜想对于任何有理数x,|x+3|+|x-6|的最小值是 .
【答案】(1)数轴上表示5的点到表示1的点的距离;(2) |x-7|;(3)7或-3 ;(4)-1,0,1,2;(5) 9 .
【解析】
(1)类比题目所给的方法解答即可;(2)类比题目所给的方法解答即可;(3)由|x-2|=5,可得x-2=5或x-2=-5,解得x=7或-3;(4)要x的整数值可以进行分段计算,令x+1=0或x-2=0时,分为3段进行计算,最后确定x的整数值;(5)由(4)的探索猜想,对于任何有理数x,|x+3|+|x-6|有最小值为9.
(1)数轴上表示5的点到表示1的点的距离.;
(2) |x-7|;
(3)7或-3 ;
(4) 令x+1=0或x-2=0时,则x=-1或x=2
当x<-1时,
∴-(x+1)-(x-2)=3,
-x-1-x+2=3,
x=-1(范围内不成立)
当-1<x<2时,
∴(x+1)-(x-2)=3,
x+5-x+2=3,
3=3,
∴x=0,1,2
当x>2时,
∴(x+1)+(x-2)=3,
x+1+x-2=7,
2x=8,
x=4(范围内不成立),
∴综上所述,符合条件的整数x有: -1,0,1,2;
(5)由(4)的探索猜想,对于任何有理数x,|x+3|+|x-6|有最小值为9.


科目:初中数学 来源: 题型:
【题目】下列3×3网格图都是由9个相同的小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:
(1)选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形;
(2)选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形;
(3)选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形.
(请将三个小题依次作答在图1、图2、图3中,均只需画出符合条件的一种情形)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若顺次连结四边形各边中点所得的四边形是矩形,则原四边形( )
A. 一定是矩形 B. 一定是菱形 C. 对角线一定相等 D. 对角线一定互相垂直
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是⊙O的内接四边形,∠ABC=2∠D,连接OC、OA、AC. 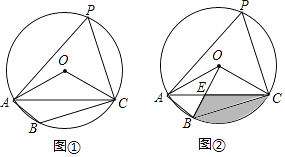
(1)如图①,求∠OCA的度数;
(2)如图②,连接OB、OB与AC相交于点E,若∠COB=90°,OC=2 ![]() ,求BC的长和阴影部分的面积.
,求BC的长和阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN是⊙O的直径,MN=4,∠AMN=30°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( ) 
A.2
B.2 ![]()
C.4 ![]()
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD为正方形,AB=![]() ,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(4,6).双曲线y= ![]() (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.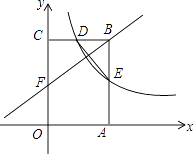
(1)求k的值及点E的坐标;
(2)若点F是边上一点,且△BCF∽△EBD,求直线FB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明有5张写着不同数的卡片,请你按照题目要求抽出卡片,完成下列问题:
(1)从中取出3张卡片,使这3张卡片上数字的乘积最大,如何抽取?最大值是多少?
(2)从中取出2张卡片,使这2张卡片上数字相除的商最小,如何抽取?最小值是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com