
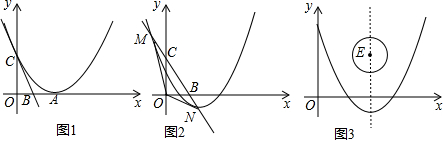
���� ��1�����������ߵĶ������깫ʽ�ó�b�������ó������߽���ʽ�����������B��C���꣬����ô���ϵ�������ֱ��BC����ʽ��
��2������ƽ�Ƶ����ʵó�ƽ�ƺ������߽���ʽ�������ó�ƽ�ƺ������ߺ�ֱ��BC�Ľ���M��N�����꣬���������ε��������ķ����������̼��ɵó����ۣ�
��3�����жϳ�PQ�ij���Сʱ����ʵ����PE��С������������ϵʽȷ����PE��Сʱ��P�����꣬�����ó���Q���꣬�������ߵ�����ȷ������һ���е㣮
��� �⣺��1����������y=$\frac{1}{2}$x2+bx+2����A��x�������ᣬ
��$\frac{4��\frac{1}{2}��2-{b}^{2}}{4��\frac{1}{2}}=0$��
��b=2���ᣩ��b=-2��
�������ߵĽ���ʽΪy=$\frac{1}{2}$x2-2x+2��
��B��1��0����C��0��2����
��ֱ��BC����ʽΪy=-2x+2��
��2����������y=$\frac{1}{2}$x2-2x+2����ƽ��k����λ��k��0����
��ƽ�ƺ�������ߵĽ���ʽy=$\frac{1}{2}$x2-2x+2-k�٣�
��ֱ��BC����ʽΪy=-2x+2�ڣ�
�����٢ڵã���M��-$\sqrt{2k}$��2$\sqrt{2k}$+2����N��$\sqrt{2k}$��-2$\sqrt{2k}$+2����
��S��MON=$\frac{1}{2}$OB����yM-yN��=$\frac{1}{2}$��1��[2$\sqrt{2k}$+2-��-2$\sqrt{2k}$+2��]=2$\sqrt{2k}$��
S��BON=$\frac{1}{2}$OB��|yN|=$\frac{1}{2}$��1����2$\sqrt{2k}$-2��=$\sqrt{2k}$-1��
��S��MON=6S��BON��
��2$\sqrt{2k}$=6��$\sqrt{2k}$-1����
��k=$\frac{9}{8}$��
��3����ͼ��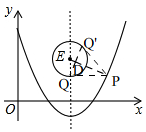 ��������y=$\frac{1}{2}$x2+bx+2�ٽ����ʵ�ƽ�ƣ�ʹƽ�ƺ�������ߵĶ���D������Ϊ��3��-1����
��������y=$\frac{1}{2}$x2+bx+2�ٽ����ʵ�ƽ�ƣ�ʹƽ�ƺ�������ߵĶ���D������Ϊ��3��-1����
��ƽ�ƺ�������߽���ʽΪy=$\frac{1}{2}$��x-3��2-1��
�������߶Գ���Ϊx=3��
�������ߵĶԳ�������һ��E����E��x��ľ���Ϊ2����E��x����Ϸ�����
��E��3��2����
��PE��PQ��EQ����ֱ�������Σ���QE=1�Ƕ�ֵ��
��ҪPQ��С��
����PE��С���ɣ�
��P��p��$\frac{1}{2}$��p-3��2-1����p��3����
��PE2=��p-3��2+[$\frac{1}{2}$��p-3��2-1-2]2=$\frac{1}{4}$[��p-3��2-4]2+5��
�൱��p-3��2=4��
��p=1���ᣩ��p=5������p=5ʱ��PE2��С������PE��С��
��P��5��1����
��PQ�С�E��Q������E�������߶Գ����·��Ľ���Ϊ��3��1�����˵��ǵ�Q��
��Q��3��1����
����Q��QQ'��PE��ԲE����һ��Q'��
��P��5��1����E��3��2������ֱ��PE�Ľ���ʽΪy=-$\frac{1}{2}$x+$\frac{7}{2}$�ۣ�
��ֱ��QQ'�Ľ���ʽΪy=2x-5�ܣ�
�����ۢܵã���D��$\frac{17}{5}$��$\frac{9}{5}$����
���Q'��m��n����
��PQ��PQ'�ǡ�E�����ߣ�
���D��QQ'���е㣬
��m+3=2��$\frac{17}{5}$��n+1=2��$\frac{9}{5}$��
��m=$\frac{19}{5}$��n=$\frac{13}{5}$��
��Q'��$\frac{19}{5}$��$\frac{13}{5}$����
����P���������5��1����Q���������3��1����$\frac{19}{5}$��$\frac{13}{5}$����
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����������ߵ����ʣ�����ϵ������ƽ�Ƶ����ʣ������ε������ʽ��Բ�����ߵ����ʣ��Լ���ֵ���⣬�Ȿ��Ĺؼ��÷��̵�˼�������⣬�������Ƚϴ���һ���ѶȱȽϴ��漰֪ʶ��Ƚ϶���п������⣮


 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
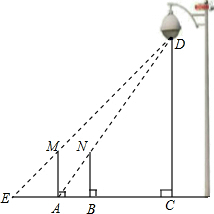 һ�����ϣ��������������õƹ��µ�Ӱ�ӳ�������һ·��D�ĸ߶ȣ���ͼ���������ߵ���A��ʱ�������������ֱ��ʱ����AM��Ӱ�ӳ�AE������ȣ�����������AC���������ǰ�ߣ��ߵ���B��ʱ������ֱ��ʱ����BN��Ӱ��ǡ�����߶�AB�������AB=1.25m����֪����ֱ��ʱ������Ϊ1.75m����·�Ƶĸ�CD�ij����������ȷ��0.1m����
һ�����ϣ��������������õƹ��µ�Ӱ�ӳ�������һ·��D�ĸ߶ȣ���ͼ���������ߵ���A��ʱ�������������ֱ��ʱ����AM��Ӱ�ӳ�AE������ȣ�����������AC���������ǰ�ߣ��ߵ���B��ʱ������ֱ��ʱ����BN��Ӱ��ǡ�����߶�AB�������AB=1.25m����֪����ֱ��ʱ������Ϊ1.75m����·�Ƶĸ�CD�ij����������ȷ��0.1m�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
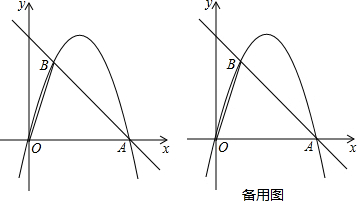
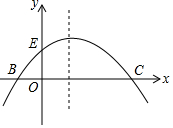 ��ͼ����֪������y=-$\frac{1}{m}$��x+2����x-m��������m��0����x�ύ�ڵ�B��C����B�ڵ�C����ࣩ����y�ύ�ڵ�E��
��ͼ����֪������y=-$\frac{1}{m}$��x+2����x-m��������m��0����x�ύ�ڵ�B��C����B�ڵ�C����ࣩ����y�ύ�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
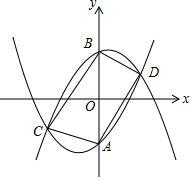 ��ƽ��ֱ������ϵ�У����ǰѹ���ԭ��ԳƵ����������߽����������á������ߣ�
��ƽ��ֱ������ϵ�У����ǰѹ���ԭ��ԳƵ����������߽����������á������ߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
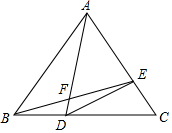 ��ͼ����ABC�ǵȱ������Σ���D�ӵ�B������BC���C�˶�����E����ͬ���ٶȴӵ�C������CA���A�˶���BE��AD�ཻ�ڵ�F������DE�������н��ۣ�����BD=$\frac{1}{3}$BC��CE=$\frac{1}{3}$AC����DE��AC����CE2=DF•DA����AF•BE=AE•AC��������ABC�ı߳�Ϊ2$\sqrt{3}$����F���D��E�˶������F�˶���������·����Ϊ4�У�������ȷ���Т٢ڢۣ�����ţ�
��ͼ����ABC�ǵȱ������Σ���D�ӵ�B������BC���C�˶�����E����ͬ���ٶȴӵ�C������CA���A�˶���BE��AD�ཻ�ڵ�F������DE�������н��ۣ�����BD=$\frac{1}{3}$BC��CE=$\frac{1}{3}$AC����DE��AC����CE2=DF•DA����AF•BE=AE•AC��������ABC�ı߳�Ϊ2$\sqrt{3}$����F���D��E�˶������F�˶���������·����Ϊ4�У�������ȷ���Т٢ڢۣ�����ţ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ������ | ����һ | ���ڶ� | ������ | ������ | ������ | ������ |
| 1 | 2 | 3 | ||||
| ������4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com