
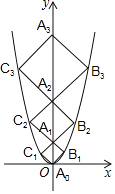
【题目】二次函数y=x2的图象如图,点A0位于坐标原点,点A1,A2,A3…An在y轴的正半轴上,点B1,B2,B3…Bn在二次函数位于第一象限的图象上,点C1,C2,C3…n在二次函数位于第二象限的图象上,四边形A0B1A1C1,四边形A1B2A2C2,四边形A2B3A3C3…四边形An﹣1BnAnn都是正方形,则正方形An﹣1BnAnn的周长为_____.
【答案】4![]() n
n
【解析】
根据四边形A0B1A1C1是正方形,可得知△A0B1A1是等腰直角三角形,结合抛物线的解析式求出△A0B1A1的直角边长,同理求出直角△A1B2A2的直角边长……,找到直角三角形△An﹣1BnAn的直角边长的规律即可求出周长.
解:∵四边形A0B1A1C1是正方形,∠A0B1A1=90°,
∴△A0B1A1是等腰直角三角形.
设△A0B1A1的直角边长为m1,则B1(![]() m,
m,![]() m);
m);
代入抛物线的解析式中得:(![]() m)2=
m)2=![]() m,
m,
解得m1=0(舍去),m1=![]() ;
;
故△A0B1A1的直角边长为![]() ,
,
同理可求得等腰直角△A1B2A2的直角边长为2![]() ,
,
…
依此类推,等腰直角△An﹣1BnAn的直角边长为![]() n,
n,
故正方形An﹣1BnAnn的周长为4![]() n.
n.
故答案是:4![]() n.
n.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
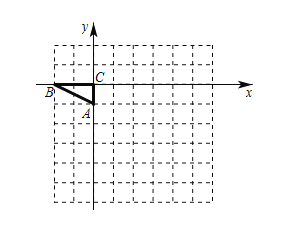
【题目】如图,平面直角坐标系中,以点C为坐标原点,点![]() ,
,![]() ,将
,将![]() 绕点A顺时针旋转90°.
绕点A顺时针旋转90°.
(1)在图中画出旋转后的![]() ,并写出点
,并写出点![]() 、
、![]() 的坐标;
的坐标;
(2)已知点![]() ,在x轴上求作一点P(注:不要求写出P点的坐标),使得PD的值最小,并求出
,在x轴上求作一点P(注:不要求写出P点的坐标),使得PD的值最小,并求出![]() 的最小值;
的最小值;
(3)写出![]() 在旋转过程中,线段AB扫过的面积
在旋转过程中,线段AB扫过的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线经过A(-1,0),B(5,0),C(0,-![]() )三点.
)三点.
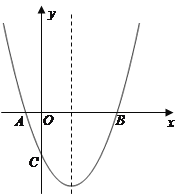
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(﹣2,1),B(1,n)两点.
的图象交于A(﹣2,1),B(1,n)两点.

(1)求反比例函数和一次函数的解析式;
(2)根据图象写出一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
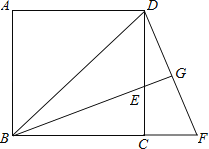
(1)求证:△BDG∽△DEG;
(2)若EGBG=4,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
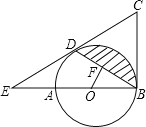
(1)求证:CD为⊙O的切线;
(2)若OF⊥BD于点F,且OF=2,BD=4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有4个大小、质地都相同的乒乓球,球面上分别标有数字1,2,3,4,小明先从布袋中随机摸出一个乒乓球,不放回去,再从剩下的3个球中随机摸出第二个乒乓球.
(1)求小明第一次摸出的乒乓球所标数字是偶数的概率;
(2)请用树状图或列表的方法求两次摸出的乒乓球球面上数字的积为偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于抛物线y=ax2+bx+c(a、b、c是常数,a≠0),若b2=ac,则称该抛物线为黄金抛物线.例如:y=x2﹣x+1是黄金抛物线
(1)请再写出一个与上例不同的黄金抛物线的解析式;
(2)将黄金抛物线y=x2﹣x+1沿对称轴向下平移3个单位
①直接写出平移后的新抛物线的解析式;
②新抛物线如图所示,与x轴交于A、B(A在B的左侧),与y轴交于C,点P是直线BC下方的抛物线上一动点,连结PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
③当直线BC下方的抛物线上动点P运动到什么位置时,四边形 OBPC的面积最大并求出此时P点的坐标和四边形OBPC的最大面积.
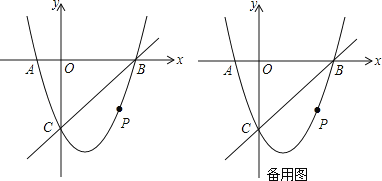
查看答案和解析>>
科目:初中数学 来源: 题型:
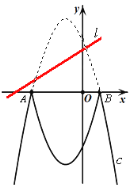
【题目】已知抛物线c:y=-x2-2x+3和直线l:y=![]() x+d。将抛物线c在x轴上方的部分沿x轴翻折180°,其余部分保持不变,翻折后的图象与x轴下方的部分组成一个“M”型的新图象(即新函数m:y=-|x2+2x-3|的图象)。
x+d。将抛物线c在x轴上方的部分沿x轴翻折180°,其余部分保持不变,翻折后的图象与x轴下方的部分组成一个“M”型的新图象(即新函数m:y=-|x2+2x-3|的图象)。
(1)当直线l与这个新图象有且只有一个公共点时,d= ;
(2)当直线l与这个新图象有且只有三个公共点时,求d的值;
(3)当直线l与这个新图象有且只有两个公共点时,求d的取值范围;
(4)当直线l与这个新图象有四个公共点时,直接写出d的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com