

分析 (1)首先证明△DGC是等腰直角三角形,在Rt△BDG中,解三角形即可解决问题.
(2)如图①中,作点G关于BD的对称点K,过K作KN⊥BC于N交BD于M,此时MG+MN=MK+MN=KN,根据垂线段最短可知,此时GM+MN最短.只要证明△KBG是等边三角形即可.
(3)存在.如图2中,PQ交DE于M.首先证明S△PQB=S△BEG+S△PEM,由此可知,△PEM的面积最小时,△BPQ的面积最小,所以P、E重合时,△PBQ面积最小,此时直线l就是直线EG.
解答 解:(1)∵四边形EFGD是矩形,
∴∠DGB=∠DGC=90°,
∵∠C=45°,
∴∠GDC=∠C=45°,
∴DG=GC=2,
∵∠ABC=60°,BD平分∠ABC,
∴∠DBG=30°,
∴BD=2GD=4,BG=$\sqrt{B{D}^{2}-D{G}^{2}}$=2$\sqrt{3}$.
故答案为2$\sqrt{3}$.
(2)如图①中,作点G关于BD的对称点K,过K作KN⊥BC于N交BD于M,此时MG+MN=MK+MN=KN,根据垂线段最短可知,此时GM+MN最短.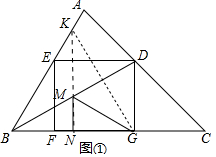
∵∠GBK=60°,BG=BK,
∴△BGK是等边三角形,KN是高,
∴KN=$\frac{\sqrt{3}}{2}$BG=$\frac{\sqrt{3}}{2}$•2$\sqrt{3}$=3.
∴GM+MN长度的最小值为3.
(3)存在.如图2中,PQ交DE于M.
∵O是EG、DF的交点,
∴EO=OG,OM=OQ,
∴S△EOB=S△OBG,S△EMO=S△OGQ,
∴S△PQB=S△PEM+S四边形EMQB=S△PEM+S四边形EBQO+S△EMO=S△PEM+S四边形EBQO+S△OQG=S△BEG+S△PEM,
∵△BEG的面积为定值,∴△PEM的面积最小时,△BPQ的面积最小,
∴P、E重合时,△PBQ面积最小,此时直线l就是直线EG,
∴△BEG的面积最小值=$\frac{1}{2}$×$2\sqrt{3}$×2=2$\sqrt{3}$.
点评 本题考查四边形综合题、解直角三角形、矩形的性质、垂线段最短等知识,解题的关键是灵活应用所学知识解决问题,学会利用对称,解决最值问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
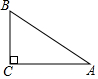 如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C出发,沿线段CA向点A运动,到达A点后停止运动,且速度为每秒2cm,设出发的时间为t秒.
如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C出发,沿线段CA向点A运动,到达A点后停止运动,且速度为每秒2cm,设出发的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
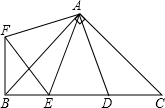 如图,在Rt△ABC 中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF.下列结论中正确的有①②③.(请将正确答案的序号填在横线上)
如图,在Rt△ABC 中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF.下列结论中正确的有①②③.(请将正确答案的序号填在横线上)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com