练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．若x1，x2是方程x2+2x-2014=0的两个根，试求下列各式的值．
    （1）x12+x22
    （2）$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$
    （3）（x1-5）（x2-5）

    分析 先将各式进行变形后，再根据根与系数的关系代入求解．

    解答 解：∵x1，x2是方程x2+2x-2014=0的两个根，
    ∴x1+x2=-2，x1x2=-2014，
    （1）x12+x22=（x1+x2）2-2x1x2=（-2）2-2×（-2014）=4032，
    （2）$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{-2}{-2014}$=$\frac{1}{1007}$，
    （3）（x1-5）（x2-5）=x1x2-5x1-5x2+25=-2014-5×（-2）+25=1979．

    点评 本题考查了一元二次方程ax2+bx+c=0（a≠0）的根与系数的关系：若方程两个为x1，x2，则x1+x2=-$\frac{b}{a}$，x1•x2=$\frac{c}{a}$．也考查了代数式的变形能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

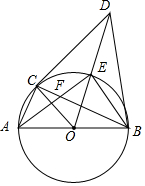    6．如图，AB为⊙O的直径，BC为⊙O的弦，过O点作OD⊥BC，交⊙O的切线CD于点D，交⊙O于点E，连接AC、AE，且AE与BC交于点F．
    （1）连接BD，求证：BD是⊙O的切线；
    （2）若AF：EF=2：1，求tan∠CAF的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．用简便方法计算：
    （1）3.68-0.82-0.18
    （2）22.5×0.48+77.5×0.48
    （3）36×（$\frac{2}{9}$+$\frac{7}{12}$）
    （4）3$\frac{2}{5}$-$\frac{1}{7}$+$\frac{3}{5}$-$\frac{6}{7}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．当m为何整数时，关于x的方程$\frac{5}{2}x$-m=$\frac{x}{2}$-3的解在1和3之间？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．设二次函数当x=3时，取最大值10，并且其图象在x轴上截得的线段长为4，求其解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．若a是方程x2-2x-1=0的解，求代数式2a2-4a+2015的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．一般地，对于一元二次方程ax2+bx+c=0（a≠0），当b2-4ac≥0时，它的根是方程有两个实数根；当b-4ac＜0时，方程方程无实数根；．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

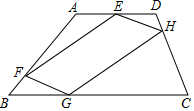    5．如图，四边形ABCD中，点E、F、G、H分别在边AD、AB、BC、DC上，且$\frac{ED}{AE}$=$\frac{BF}{AF}$=$\frac{BG}{GC}$=+$\frac{DH}{CH}$=$\frac{1}{2}$
    （1）求证：EFGH为平行四边形
    （2）当ABCD的对角线AC与BD有怎样的数量关系时，EFGH为菱形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．海中有A、B、C三个小岛，A岛在B岛正西方距离400海里处（如图所示），C岛在B岛的北偏东37°方向500海里处．

    （1）用1厘米代表200海里，请根据题意在图中画出C岛的位置；量出图中AC的长度为4厘米．（四舍五入到整厘米数）；那么A、C两地的实际距离约为800海里．
    （2）甲、乙两货轮同时从A岛出发，甲沿A-C-B方向，乙沿A-B-C方向，10小时相遇，此时甲货轮比乙货轮多行驶了100海里，求甲乙两货轮的速度．
    （3）若B岛需要大米和玉米共30吨，C岛需要大米和玉米共50吨，现从A岛运输20吨大米与60吨玉米到B岛和C岛，运输费用共为10600元（每吨的运输费用如下表所示）那么运到B岛的大米与玉米各是多少吨？：
    到B岛的运费（元/吨）到C岛的运费（元/吨）
    大米100200
    玉米80150

    查看答案和解析>>

    同步练习册答案