
【题目】《重庆市生活垃圾分类管理办法》于2019年开始实施我校为积极响应政府对垃圾分类处理的号召,开展了垃圾分类网上知识竞赛,并从该校七年级随机抽取了部分学生的竞赛成绩进行整理、描述和分析(根据成绩共分![]() 四个等级),其中获得
四个等级),其中获得![]() 等级和
等级和![]() 等级的人数相等.
等级的人数相等.
下面给出了相应的条形统计图和扇形统计图:

根据以上信息,解答下列问题:
(1)共抽取了______名学生;
(2)补全条形统计图,并求出扇形统计图中![]() 等级对应的圆心角的度数;
等级对应的圆心角的度数;
(3)A等级中有![]() 名同学是女生,学校计划从
名同学是女生,学校计划从![]() 等级的学生中抽取
等级的学生中抽取![]() 名参加区级垃圾分类网上知识竞赛,则抽到女生的概率是多少?
名参加区级垃圾分类网上知识竞赛,则抽到女生的概率是多少?
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】某文化用品商店用2000元购进一批学生书包,面市后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了4元,结果第二批用了6300元.
(1)求第一批购进书包的单价是多少元?
(2)若商店销售这两批书包时,每个售价都是120元,全部售出后,商店共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 ,是一个8×10正方形格纸,△ABC中A点坐标为(-2,1).
(1)补全坐标系并指出△ABC和△A'B'C'满足什么几何变换(直接写答案)?
(2)作△A'B'C'关于x轴对称图形△A''B''C'';
(3)△ABC和△A''B''C''满足什么几何变换?求A''、B''、C''三点坐标(直接写答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC向右平移3个单位长度,再向上平移2个单位长度,可以得到![]() .
.

(1)画出平移后的![]() ;
;
(2)写出![]() 三个顶点的坐标;
三个顶点的坐标;
(3)已知点P在x轴上,以![]() 、
、![]() 、P为顶点的三角形面积为4,求点P的坐标.
、P为顶点的三角形面积为4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
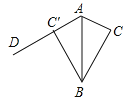
【题目】如图,△ABC的面积为6,AC3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的![]() 处,P为直线AD上的任意一点,则线段BP的最短长度为_____________.
处,P为直线AD上的任意一点,则线段BP的最短长度为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某小区实施供暖改造工程,现甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中,正确的个数有( )个.
①甲队每天挖100米;
②乙队开挖两天后,每天挖50米;
③当x=4时,甲、乙两队所挖管道长度相同;
④甲队比乙队提前2天完成任务.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=(x﹣1)2+k分别与x轴、y轴交于A、B、C三点,点A在点B的左侧,直线y=﹣ ![]() x+2经过点B,且与y轴交于点D.
x+2经过点B,且与y轴交于点D.
(1)如图1,求k的值;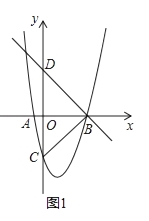
(2)如图2,在第一象限的抛物线上有一动点P,连接AP,过P作PE⊥x轴于点E,过E作EF⊥AP于点F,过点D作平行于x轴的直线分别与直线FE、PE交于点G、H,设点P的横坐标为t,线段GH的长为d,求d与t的函数关系式,并直接写出t的取值范围;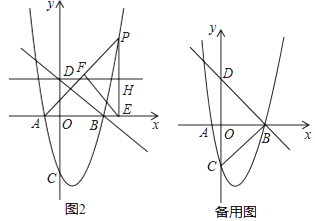
(3)在(2)的条件下,过点G作平行于y轴的直线分别交AP、x轴和抛物线于点M、T和N,tan∠MEA= ![]() ,点K为第四象限抛物线上一点,且在对称轴左侧,连接KA,在射线KA上取一点R,连接RM,过点K作KQ⊥AK交PE的延长线于Q,连接AQ、HK,若∠RAE﹣∠RMA=45°,△AKQ与△HKQ的面积相等,求点R的坐标.
,点K为第四象限抛物线上一点,且在对称轴左侧,连接KA,在射线KA上取一点R,连接RM,过点K作KQ⊥AK交PE的延长线于Q,连接AQ、HK,若∠RAE﹣∠RMA=45°,△AKQ与△HKQ的面积相等,求点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为( )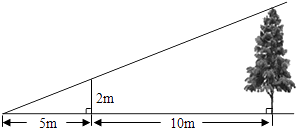
A.5m
B.6m
C.7m
D.8m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com