
分析 (1)原式利用零指数幂、负整数指数幂法则,以及乘方的意义计算即可得到结果;
(2)原式利用幂的乘方及积的乘方运算法则,以及单项式乘以多项式法则计算,合并即可得到结果;
(3)原式利用平方差公式,以及完全平方公式化简,去括号合并即可得到结果;
(4)原式利用平方差公式计算即可得到结果.
解答 解:(1)原式=$\frac{1}{4}$-1+$\frac{9}{4}$=$\frac{5}{2}$-1=$\frac{3}{2}$;
(2)原式=am+2+am+2=2am+2;
(3)原式=x2-y2-x2+2xy-y2=2xy-2y2;
(4)原式=(x2-1)(x2+1)=x4-1.
点评 此题考查了整式的混合运算,以及实数的运算,熟练掌握运算法则是解本题的关键.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
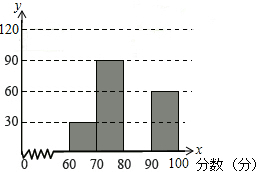 某校举行了一场学生“安全知识”问答竞赛活动,为了解笔试情况,随机抽查了部分学生的得分情况,请根据图表提供的信息,解答下列问题:
某校举行了一场学生“安全知识”问答竞赛活动,为了解笔试情况,随机抽查了部分学生的得分情况,请根据图表提供的信息,解答下列问题:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.1 |
| 70≤x<80 | 90 | n |
| 80≤x<90 | m | 0.4 |
| 90≤x<100 | 60 | 0.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.443×1010 | B. | 4.43×109 | C. | 443×108 | D. | 4.43×1010 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
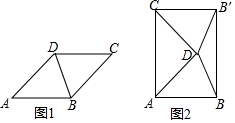
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com