
分析 先分别计算:①$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}$=1+$\frac{1}{1}$-$\frac{1}{2}$,②$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}$=1+$\frac{1}{2}$-$\frac{1}{3}$,③$\sqrt{1+\frac{1}{{3}^{2}}+\frac{1}{{4}^{2}}}$=1+$\frac{1}{3}$-$\frac{1}{4}$,…④$\sqrt{1+\frac{1}{201{5}^{2}}+\frac{1}{201{6}^{2}}}$=1+$\frac{1}{2015}$-$\frac{1}{2016}$,再依次计算S1、S2、S3、…、S2016的值,从而得出结论.
解答 解:∵$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}$=1+$\frac{1}{1}$-$\frac{1}{2}$,
$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}$=1+$\frac{1}{2}$-$\frac{1}{3}$,
$\sqrt{1+\frac{1}{{3}^{2}}+\frac{1}{{4}^{2}}}$=1+$\frac{1}{3}$-$\frac{1}{4}$,
…
∴$\sqrt{1+\frac{1}{201{5}^{2}}+\frac{1}{201{6}^{2}}}$=1+$\frac{1}{2015}$-$\frac{1}{2016}$,
∴S1=$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}$=1+$\frac{1}{1}$$-\frac{1}{2}$,
S2=$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}$+$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}$=(1$+\frac{1}{1}-\frac{1}{2}$)+(1$+\frac{1}{2}-\frac{1}{3}$),
S3=$\sqrt{1+\frac{1}{{1}^{2}}+\frac{1}{{2}^{2}}}$+$\sqrt{1+\frac{1}{{2}^{2}}+\frac{1}{{3}^{2}}}$+$\sqrt{1+\frac{1}{{3}^{2}}+\frac{1}{{4}^{2}}}$=(1+$\frac{1}{1}$-$\frac{1}{2}$)+(1$+\frac{1}{2}-\frac{1}{3}$)+(1$+\frac{1}{3}-\frac{1}{4}$),
…
∴S2016=(1+$\frac{1}{1}$-$\frac{1}{2}$)+(1$+\frac{1}{2}-\frac{1}{3}$)+(1$+\frac{1}{3}-\frac{1}{4}$)+…+(1+$\frac{1}{2015}$-$\frac{1}{2016}$)+(1+$\frac{1}{2016}$-$\frac{1}{2017}$),
=2016+1-$\frac{1}{2017}$,
=2016+$\frac{2016}{2017}$,
∴则$\frac{{S}_{2016}}{2016}$=$\frac{2016+\frac{2016}{2017}}{2016}$=1+$\frac{1}{2017}$=$\frac{2018}{2017}$.
点评 本题是二次根式的化简求值,也是利用简便算法进行计算的问题;考查了学生理解能力和相反数的意义;根据已知所给的式子找规律并进行计算,还利用了互为相反数的和为零化简求值.


 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
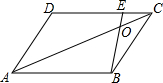 如图平行四边形ABCD中,E为DC上一点,且CE=3,AB=9,对角线AC与BE相交于点O,则S△EOC:S△ABC为( )
如图平行四边形ABCD中,E为DC上一点,且CE=3,AB=9,对角线AC与BE相交于点O,则S△EOC:S△ABC为( )| A. | 1:6 | B. | 1:9 | C. | 1:13 | D. | 1:12 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
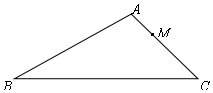 如图,在△ABC中,AB=8,AC=5,M是AC边上的一点,AM=2,在AB边上取一点N,使以A、M、N为顶点的三角形与△ABC相似,则AN的长为$\frac{16}{5}$或$\frac{5}{4}$.
如图,在△ABC中,AB=8,AC=5,M是AC边上的一点,AM=2,在AB边上取一点N,使以A、M、N为顶点的三角形与△ABC相似,则AN的长为$\frac{16}{5}$或$\frac{5}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com