
如图10,C是线段AB上的一点,△ACD和△BCE都是等边三角形.
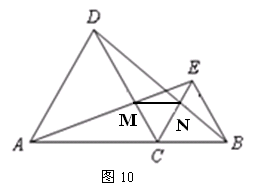
(1)求证:AE=BD;
(2)若AE交CD于M,BD交CE于N,连结MN,试判断△MCN的形状,并说明理由.
(1)证明略
(2)等边三角形,理由略
解析:(1)证明:∵△ACD和△BCE都是等边三角形
∴AC=CD,CE=CB,∠ACD=∠BCE=60°…………………………………1分
∵∠ACD+∠DCE=∠BCE+∠DCE
∴∠ACE=∠DCB………………………………………………………………2分
∴△ACE≌△DCB
∴AE=BD…………………………………………………………………………3分
(2)△MCN是等边三角形…………………………………………………………4分
∵∠ACD=∠BCE=60°,∠ACB是一个平角
∴∠DCE=60°
即∠ACM=∠DCN…………………………………………………………………5分
由(1)得△ACE≌△DCB
∴∠CAM=∠CDN…………………………………………………………………6分
又AC=DC
∴△ACM≌△DCN…………………………………………………………………7分



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011年江苏省姜堰市初一第一学期期末考试数学卷 题型:解答题
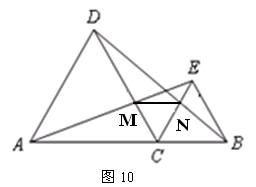
如图10,C是线段AB上的一点,△ACD 和△BCE都是等边三角形.
和△BCE都是等边三角形.
 (1)求证:AE=BD;
(1)求证:AE=BD;
(2)若AE交CD于M,BD交CE于N,连结MN,试判断△MCN的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2011年江苏省姜堰市初一第一学期期末考试数学卷 题型:解答题
如图10,C是线段AB上的一点,△ACD和△BCE都是等边三角形.
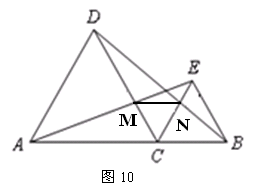
(1)求证:AE=BD;
(2)若AE交CD于M,BD交CE于N,连结MN,试判断△MCN的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com