
分析 (1)设x小时后相距660千米,等量关系为:慢车x小时的路程+快车x小时的路程=660千米-408千米,列出方程求出x的值;
(2)设快车开出y小时后两车相遇,等量关系为:慢车(y+1)小时的路程+快车y小时的路程=408千米,列方程求出y的值.
解答 解:(1)设x小时后,两车相距660千米.
根据题意,得72x+408+96x=660.
移项,得72x+96x=660-408
化简,得168x=252 所以 x=1.5
答:1.5小时后两车相距660千米.
(2)设快车开出后y小时两车相遇.
根据题意,得72+72y+96y=408
移项,得72x+96x=408-72
化简,得168x=336 所以 y=2
答:快车开出2小时后两车相遇.
点评 本题考查了一元一次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.


科目:初中数学 来源: 题型:解答题
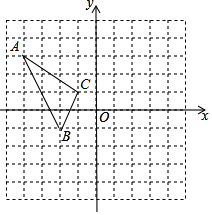 如图,在平面直角坐标系中,△ABC的顶点A(-4,3),B(-2,-1),C(-1,1)均在正方形网格的格点上,画出△ABC关于y轴对称的△A1B1C1,并写出点A的对应点A1的坐标.
如图,在平面直角坐标系中,△ABC的顶点A(-4,3),B(-2,-1),C(-1,1)均在正方形网格的格点上,画出△ABC关于y轴对称的△A1B1C1,并写出点A的对应点A1的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
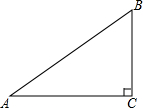 如图,Rt△ABC中,∠C=90°,AC=4,BC=3,则tanA的值为( )
如图,Rt△ABC中,∠C=90°,AC=4,BC=3,则tanA的值为( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
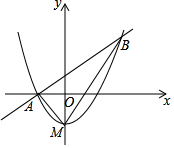 如图,顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.
如图,顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
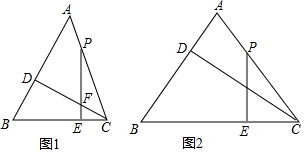
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
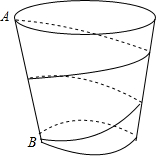 如图,一只杯子的上下底面分别是直径为5cm和7.5cm的圆,母线AB的长为15cm.
如图,一只杯子的上下底面分别是直径为5cm和7.5cm的圆,母线AB的长为15cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com