练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．如图，有多个长方形和正方形的卡片，图甲是选取了2块不同的卡片，拼成的一个图形，借助图中阴影部分面积的不同表示可以用来验证恒等式a（a+b）=a2+ab成立．
    （1）根据图乙，利用面积的不同表示方法，写出一个代数恒等式（a+2b）（a+b）=a2+3ab+2b2；
    （2）试将等式（a+b）2=a2+2ab+b2补充完整，并用上述拼图的方法说明它的正确性．

    分析 （1）根据图形是一个长方形求出长和宽，相乘即可；
    （2）正方形的面积是2个长方形的面积加上2个正方形的面积，代入求出即可．

    解答 解：（1）观察图乙得知：长方形的长为：a+2b，宽为a+b，
    ∴面积为：（a+2b）（a+b）=a2+3ab+2b2；　　
    故答案为：（a+2b）（a+b）=a2+3ab+2b2
    （2）如图所示：恒等式是，（a+b）（a+b）=a2+2ab+b2．
    答：恒等式是（a+b）（a+b）=a2+2ab+b2．
    故答案为：a2+2ab+b2．

    点评 本题主要考查对多项式乘多项式的理解和掌握，能表示各部分的面积是解此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    7．某中学为了解学生到校交通方式情况，随机抽取各年级部分学生就“上下学交通方式”进行问卷调查，调查分为“A：骑自行车；B：不行；C：坐公交车；D：其他”四种情况，并根据调查结果绘制出部分条形统计图（如图1）和部分扇形统计图（如图2），请根据图中的信息，解答下列问题：
    （1）本次调查共抽取100名学生；
    （2）求出扇形统计图中“C”所对扇形的圆心角的度数，并将条形统计图补充完整；
    （3）若该中学共有学生3000人，估计有多少学生在上下学交通方式中选择坐公交车？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．解不等式组$\left\{\begin{array}{l}{3（x+1）＜2x+3}\\{\frac{x-1}{3}≤\frac{2}{x}}\end{array}\right.$，并在数轴上表示它们的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．若a、b满足|a-2|+$\sqrt{b+1}$=0，求代数式$\frac{{b}^{3}}{{a}^{2}}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

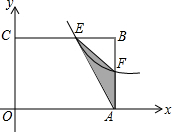    12．如图，在矩形OABC中，OA=3，OC=2，F是AB上的一个动点（F不与A，B重合），过点F的反比例函数y=$\frac{k}{x}$（k＞0）的图象与BC边交于点E．
    （1）当F为AB的中点时，求该函数的解析式；
    （2）当k为何值时，△EFA的面积为$\frac{2}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．甲乙两地相距72千米，李磊骑自行车往返两地一共用了7小时，已知他去时的平均速度比返回时的平均速度快$\frac{1}{3}$，求李磊去时的平均速度是多少？
    小芸同学解法如下：
    解：设李磊去时的平均速度是x千米/时，则返回时的平均速度是（1-$\frac{1}{3}$）x千米/时，由题意得：$\frac{72}{x}$+$\frac{72}{（1-\frac{1}{3}）x}$=7，…
    你认为小芸同学的解法正确吗？若正确，请写出该方程所依据的等量关系，并完成剩下的步骤；若不正确，请说明原因，并完整地求解问题．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．计算：
    （1）$\sqrt{25}$-$\root{3}{27}$+$\sqrt{\frac{1}{4}}$；
    （2）$\sqrt{（-2）^{2}}$+|$\sqrt{2}$-1|-（$\sqrt{2}$+1）．
    （3）（-$\frac{1}{2}$）2+$\frac{3}{4}$-（2-$\sqrt{3}$）+|2-$\sqrt{3}$|

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图1，菱形ABCD中，AB=10，连接BD，tan∠ABD=$\frac{1}{2}$，若P是射线BC上的一个动点（点P不与点B重合），连接AP，与对角线相交于点E，连接EC．
    （1）求证：AE=CE；
    （2）当点P在线段BC上时，设BP=x，S△EPC=y，求y关于x的函数解析式，并写出x的取值范围；
    （3）当点P在线段BC的延长线上时，若△EPC是直角三角形，求线段BP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．如图，在菱形ABCD中，∠B=120°，AB=4，点E是BC的中点，点F在CD边上，点C关于EF的对称点为C′，连接EC′，FC′，当点F从C运动到点D的过程中，AC′长度的最大值与最小值的差为4$\sqrt{3}$-2$\sqrt{7}$+2．

    查看答案和解析>>

    同步练习册答案