
【题目】某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如下两个不完整的统计图(校服型号以身高作为标准,共分为6种型号).
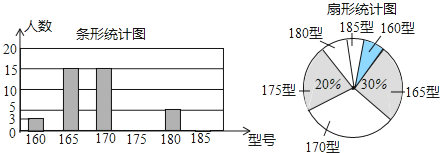
根据以上信息,解答下列问题:
(Ⅰ)该班共有 名学生,其中穿175型校服的学生有 名;
(Ⅱ)在条形统计图中,请把空缺部分补充完整.
(Ⅲ)在扇形统计图中,185型校服所对应的扇形圆心角的大小为 ;
(Ⅳ)该班学生所穿校服型号的众数为 ,中位数为 .
(Ⅴ)如果该校预计招收新生600名,根据样本数据,估计新生中穿170型校服的学生大约有 名.
【答案】(Ⅰ)50,10;(Ⅱ)补图见解析;(Ⅲ)14.4°;(Ⅳ)165和170,170;(Ⅴ)180.
【解析】
试题(Ⅰ)根据穿165型的人数与所占的百分比列式进行计算即可求出学生总人数,再乘以175型所占的百分比计算即可得解;
(Ⅱ)先求出185型的人数,然后补全统计图;
(Ⅲ)用185型所占的百分比乘以360°计算即可得解;
(Ⅳ)根据众数的定义以及中位数的定义解答;
(Ⅴ)用招收新生600名乘以新生中穿170型校服的学生所占的百分比,即可求出答案.
试题解析:(Ⅰ)根据题意得:
15÷30%=50(名),
50×20%=10(名),
答:该班共有50名学生,其中穿175型校服的学生有10名;
(Ⅱ)185型的学生人数为:50-3-15-15-10-5=50-48=2(名),
补全统计图如图所示:
(Ⅲ)185型校服所对应的扇形圆心角为:![]() ×360°=14.4°;
×360°=14.4°;
(Ⅳ)165型和170型出现的次数最多,都是15次,则众数是165和170;
共有50个数据,第25、26个数据都是170,则中位数是170.
(Ⅴ)根据题意得:600×![]() =180(名),
=180(名),
答:新生中穿170型校服的学生大约有180名.


科目:初中数学 来源: 题型:
【题目】小明和他的同学根据抛掷两枚硬币时记录的实验结果,制作“出现两个正面”的频数、频率表如下:
抛掷次数 |
|
|
|
|
|
|
|
| |
出现两个正面的频数 |
|
|
|
|
|
|
|
| |
出现两个正面的频率 |
|
|
|
|
|
|
|
|
![]() 在大数次抛掷两枚硬币的实验中,出现两个正面的频率稳定在________附近;
在大数次抛掷两枚硬币的实验中,出现两个正面的频率稳定在________附近;
![]() 小明和表弟玩一个抛掷两枚硬币的游戏,小明制定的游戏规则如下:抛出两个正面–小明的表弟赢
小明和表弟玩一个抛掷两枚硬币的游戏,小明制定的游戏规则如下:抛出两个正面–小明的表弟赢![]() 分;抛出其他结果–小明赢
分;抛出其他结果–小明赢![]() 分;谁先到
分;谁先到![]() 分,谁就得胜.你认为这个游戏规则公平吗?说说理由.
分,谁就得胜.你认为这个游戏规则公平吗?说说理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象与x轴交于点(﹣2,0)、(x1,0),且1<x1<2,与y轴正半轴的交点在(0,2)的下方,在原点的上方.下列结论:①4a﹣2b+c=0;②2a﹣b<0;③2a﹣b>﹣1;④2a+c<0;⑤b>a;其中正确结论的个数是( )
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知△ABC中,AB=10cm,AC=8cm,BC=6cm.如果点P由B出发沿BA方向点A匀速运动,同时点Q由A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤4).解答下列问题:
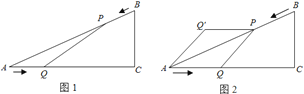
(1)当t为何值时,PQ∥BC.
(2)设△AQP面积为S(单位:cm2),当t为何值时,S取得最大值,并求出最大值.
(3)是否存在某时刻t,使线段PQ恰好把△ABC的面积平分?若存在,求出此时t的值;若不存在,请说明理由.
(4)如图2,把△AQP沿AP翻折,得到四边形AQPQ′.那么是否存在某时刻t,使四边形AQPQ′为菱形?若存在,求出此时菱形的面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由边长为1的小正方形组成的![]() 网格,直线
网格,直线![]() 是一条网格线,点
是一条网格线,点![]() ,
,![]() 在格点上,
在格点上,![]() 的三个顶点都在格点(网格线的交点)上.
的三个顶点都在格点(网格线的交点)上.

(1)作出![]() 关于直线
关于直线![]() 对称的
对称的![]() ;
;
(2)在直线![]() 上画出点
上画出点![]() ,使四边形
,使四边形![]() 的周长最小;
的周长最小;
(3)在这个![]() 网格中,到点
网格中,到点![]() 和点
和点![]() 的距离相等的格点有_________个.
的距离相等的格点有_________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解学生对新闻、体育、娱乐、动画四类电视节目的喜爱情况,进行了统计调查![]() 随机调查了某班所有同学最喜欢的节目
随机调查了某班所有同学最喜欢的节目![]() 每名学生必选且只能选择四类节目中的一类
每名学生必选且只能选择四类节目中的一类![]() 并将调查结果绘成如下不完整的统计图
并将调查结果绘成如下不完整的统计图![]() 根据两图提供的信息,回答下列问题:
根据两图提供的信息,回答下列问题:
![]() 最喜欢娱乐类节目的有______人,图中
最喜欢娱乐类节目的有______人,图中![]() ______;
______;
![]() 请补全条形统计图;
请补全条形统计图;
![]() 根据抽样调查结果,若该校有1800名学生,请你估计该校有多少名学生最喜欢娱乐类节目;
根据抽样调查结果,若该校有1800名学生,请你估计该校有多少名学生最喜欢娱乐类节目;
![]() 在全班同学中,有甲、乙、丙、丁等同学最喜欢体育类节目,班主任打算从甲、乙、丙、丁4名同学中选取2人参加学校组织的体育知识竞赛,请用列表法或树状图求同时选中甲、乙两同学的概率.
在全班同学中,有甲、乙、丙、丁等同学最喜欢体育类节目,班主任打算从甲、乙、丙、丁4名同学中选取2人参加学校组织的体育知识竞赛,请用列表法或树状图求同时选中甲、乙两同学的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某服装厂现有![]() 种布料70米,
种布料70米,![]() 种布料52米,现计划用这两种布料生产
种布料52米,现计划用这两种布料生产![]() 、
、![]() 两种型号的时装共80套.已知做一套
两种型号的时装共80套.已知做一套![]() 型号的时装需用A种布料1.1米,
型号的时装需用A种布料1.1米,![]() 种布料0.4米,可获利50元;做一套
种布料0.4米,可获利50元;做一套![]() 型号的时装需用
型号的时装需用![]() 种布料0.6米,
种布料0.6米,![]() 种布料0.9米,可获利45元.设生产
种布料0.9米,可获利45元.设生产![]() 型号的时装套数为
型号的时装套数为![]() ,用这批布料生产两种型号的时装所获得的总利润为
,用这批布料生产两种型号的时装所获得的总利润为![]() 元.
元.
(1)求![]() (元)与
(元)与![]() (套)的函数关系式.
(套)的函数关系式.
(2)有几种生产方案?
(3)如何生产使该厂所获利润最大?最大利润是多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,若动点
,若动点![]() 从点
从点![]() 开始,按
开始,按![]() 的路径运动,且速度为每秒
的路径运动,且速度为每秒![]() ,设出发的时间为
,设出发的时间为![]() 秒.
秒.

(1)出发2秒后,求![]() 的周长.
的周长.
(2)问![]() 为何值时,
为何值时,![]() 为等腰三角形?
为等腰三角形?
(3)另有一点![]() ,从点
,从点![]() 开始,按
开始,按![]() 的路径运动,且速度为每秒
的路径运动,且速度为每秒![]() ,若
,若![]() 、
、![]() 两点同时出发,当
两点同时出发,当![]() 、
、![]() 中有一点到达终点时,另一点也停止运动.当
中有一点到达终点时,另一点也停止运动.当![]() 为何值时,直线
为何值时,直线![]() 把
把![]() 的周长分成
的周长分成![]() 的两部分?
的两部分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列动车从A地开往B地,一列普通列车从B地开往A地,两车均匀速行驶并同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),如图中的折线表示y与x之间的函数关系,下列说法中正确的是:( )
①AB两地相距1000千米;②两车出发后3小时相遇;③普通列车的速度是100千米/小时;④动车从A地到达B地的时间是4小时.
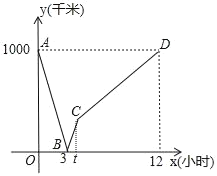
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com