练习册

  • 练习册
  • 试题
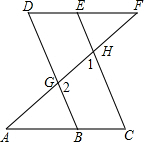
    精英家教网 > 初中数学 > 题目详情
    精英家教网如图：点E在直线DF上，点B在直线AC上，∠1=70°，∠2=110°，∠C=∠D．试问：∠A=∠F吗？请你说明理由．
    分析：首先根据平行四边形的判定得出BD∥EC，进而根据平行四边形的性质得出∠D=∠DBA，即可得出DF∥AC，进而得出答案．
    解答：解：∠A=∠F，
    理由：∵∠1=70°，∠2=110°，
    ∴BD∥EC，
    ∴∠C=∠DBA，
    ∵∠D=∠C，
    ∴∠D=∠DBA，
    ∴DF∥AC，
    ∴∠A=∠F．
    点评：此题主要考查了平行线的判定与性质，根据已知得出DF∥AC是解题关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

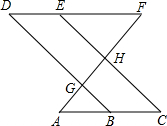    如图，点E在直线DF上，点B在直线AC上，若∠AGB=∠EHF，∠C=∠D．
    则∠A=∠F，请说明理由．
    解：∵∠AGB=∠EHF
    已知
    已知

    ∠AGB=
    ∠DGF
    ∠DGF
    （对顶角相等）
    ∴∠EHF=∠DGF
    ∴DB∥EC
    同位角相等，两直线平行
    同位角相等，两直线平行

    ∴∠
    C
    C
    =∠DBA （ 两直线平行，同位角相等）
    又∵∠C=∠D
    ∴∠DBA=∠D
    ∴DF∥
    AC
    AC
    （内错角相等，两直线平行）
    ∴∠A=∠F
    两直线平行，内错角相等
    两直线平行，内错角相等
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

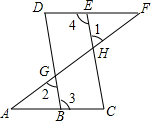    如图，点E在直线DF上，点B在直线AC上，若∠1=∠2，∠3=∠4，则∠A=∠F，请说明理由．
    解：∵∠1=∠2（已知）
    ∠2=∠DGF
    （对顶角相等）
    （对顶角相等）

    ∴∠1=∠DGF
    ∴BD∥CE
    （同位角相等，两直线平行）
    （同位角相等，两直线平行）

    ∴∠3+∠C=180°
    （两直线平行，同旁内角互补）
    （两直线平行，同旁内角互补）

    又∵∠3=∠4（已知）
    ∴∠4+∠C=180°
    ∴
    DF
    DF
    ∥
    AC
    AC
    （同旁内角互补，两直线平行）
    ∴∠A=∠F
    （两直线平行，内错角相等）
    （两直线平行，内错角相等）
    ．

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年浙江省建德市李家镇初级中学七年级下学期期中数学卷（带解析） 题型：填空题

    如图，点E在直线DF上，点B在直线AC上，若∠1＝∠2，∠3＝∠4，则∠A＝∠F，请说明理由．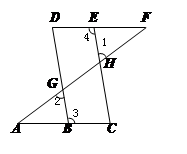

    解：∵∠1＝∠2（已知）
    ∠2＝∠DGF（ ）
    ∴∠1＝∠DGF
    ∴BD∥CE（ ）
    ∴∠3＋∠C＝180º（ ）
    又∵∠3＝∠4（已知）
    ∴∠4＋∠C＝180º
    ∴       ∥       （同旁内角互补，两直线平行）
    ∴∠A＝∠F（ ）

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年湖北天门七年级下学期期末考试数学试卷（解析版） 题型：解答题

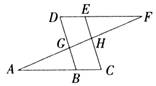
    如图，点E在直线DF上，点B在直线AC上，DB、EC分别交AF于点G、H，若∠AGB=∠EHF，∠C=∠D，请你判断∠A和∠F的大小关系，并说明你的理由．

      

     

    查看答案和解析>>

    同步练习册答案