
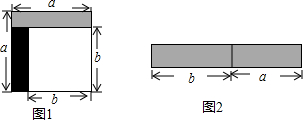
 从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).分析 (1)观察图1与图2,根据两图形阴影部分面积相等,验证平方差公式即可;
(2)①已知第一个等式左边利用平方差公式化简,将第二个等式代入求出所求式子的值即可;②先利用平方差公式变形,再约分即可得到结果.
解答 解:(1)根据图形得:a2-b2=(a+b)(a-b),
上述操作能验证的等式是B,
故答案为:B;
(2)①∵x2-4y2=(x+2y)(x-2y)=12,x+2y=4,
∴x-2y=12÷4=3;
②(1-$\frac{1}{{2}^{2}}$)(1-$\frac{1}{{3}^{2}}$)(1-$\frac{1}{{4}^{2}}$)…(1-$\frac{1}{201{5}^{2}}$)(1-$\frac{1}{201{6}^{2}}$)
=(1-$\frac{1}{2}$)(1+$\frac{1}{2}$)(1-$\frac{1}{3}$)(1+$\frac{1}{3}$)…(1-$\frac{1}{2015}$)(1+$\frac{1}{2015}$)(1-$\frac{1}{2016}$)(1+$\frac{1}{2016}$)
=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$×$\frac{3}{4}$×…×$\frac{2014}{2015}$×$\frac{2016}{2015}$×$\frac{2015}{2016}$×$\frac{2017}{2016}$
=$\frac{1}{2}$×$\frac{2017}{2016}$
=$\frac{2017}{4032}$.
点评 此题考查了平方差公式的几何背景以及因式分解法的运用,熟练掌握平方差公式的结构特征是解本题的关键.


科目:初中数学 来源: 题型:解答题
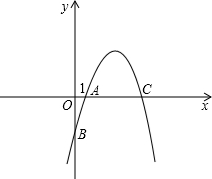 如图,抛物线y=-x2+5x+n与x轴交点A(1,0),另一交点C,与y轴交于点B.
如图,抛物线y=-x2+5x+n与x轴交点A(1,0),另一交点C,与y轴交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
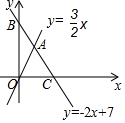 如图,直线y=-2x+7与x轴、y轴分别相交于点C、B,与直线y=$\frac{3}{2}$x相交于点A.
如图,直线y=-2x+7与x轴、y轴分别相交于点C、B,与直线y=$\frac{3}{2}$x相交于点A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将图中的△ABC作如下运动:
将图中的△ABC作如下运动:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
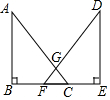 如图,△ABC和△DEF为直角三角形,∠ABC=∠DEF=90°,边BC、EF在同一直线上,斜边AC、DF交于点G,且BF=CD,AC=DF.求证:GF=GC.
如图,△ABC和△DEF为直角三角形,∠ABC=∠DEF=90°,边BC、EF在同一直线上,斜边AC、DF交于点G,且BF=CD,AC=DF.求证:GF=GC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com