
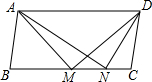
 如图,平行四边形ABCD中,M、N是BC边上的点,且∠AMD=∠AND=90°,则下列结论中一定成立的是(1)(3)(4)(把所有正确结论的序号都填在横线上)
如图,平行四边形ABCD中,M、N是BC边上的点,且∠AMD=∠AND=90°,则下列结论中一定成立的是(1)(3)(4)(把所有正确结论的序号都填在横线上)分析 先证明A、M、N、D四点共圆,由圆周角定理得出∠NAD=∠DMN,由平行四边形的性质得出∠ADM=∠DMN,得出∠NAD=∠ADM,(1)成立;由圆周角定理得出$\widehat{AM}=\widehat{DN}$,证出AM=DN,(4)成立;得出四边形AMND是等腰梯形,由等腰梯形的性质得出AN=DM,(3)成立;不能得出BM=MC,②不一定成立;即可得出结果.
解答 解:结论中一定成立的是:(1)(3)(4);理由如下:
∵∠AMD=∠AND=90°,
∴A、M、N、D四点共圆,
∴∠NAD=∠DMN,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠ADM=∠DMN,
∴∠NAD=∠ADM,(1)成立;
∴$\widehat{AM}=\widehat{DN}$,
∴AM=DN,(4)成立;
∴四边形AMND是等腰梯形,
∴AN=DM,(3)成立.
没有条件证出BM=MC;
故答案为:(1)(3)(4).
点评 本题考查了平行四边形的性质、四点共圆、圆周角定理、等腰梯形的判定与性质等知识;熟练掌握圆周角定理和平行四边形的性质,证明四点共圆是解决问题的关键.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
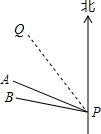 如图,台风中心位于点P处,并沿北偏西30°方向PQ移动,已知台风中心移动的速度是30km/h,受台风影响区域的半径为200km.A市位于点P的北偏西60°方向上,与点P的距离为200$\sqrt{3}$km处;B市位于点P的北偏西75°方向上,与点P的距离为210$\sqrt{2}$km处.
如图,台风中心位于点P处,并沿北偏西30°方向PQ移动,已知台风中心移动的速度是30km/h,受台风影响区域的半径为200km.A市位于点P的北偏西60°方向上,与点P的距离为200$\sqrt{3}$km处;B市位于点P的北偏西75°方向上,与点P的距离为210$\sqrt{2}$km处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知直线m,n之间的距离是3,△ABC的顶点A在直线m上,边BC在直线n上,求△ABC的面积S和BC边的长x之间的关系式,并指出其中的变量和常量.
已知直线m,n之间的距离是3,△ABC的顶点A在直线m上,边BC在直线n上,求△ABC的面积S和BC边的长x之间的关系式,并指出其中的变量和常量.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com