
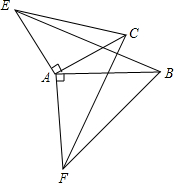
 如图,△ACE,△ABF都是等腰直角三角形.∠BAF=∠CAE=90°.那么图中哪一个三角形绕着什么点旋转多少度能与另一个三角形重合.
如图,△ACE,△ABF都是等腰直角三角形.∠BAF=∠CAE=90°.那么图中哪一个三角形绕着什么点旋转多少度能与另一个三角形重合.  天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
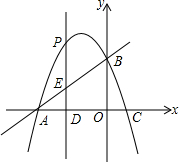 在平面直角坐标系中,直线y=x+4与x轴分别交于A、B两点,抛物线y=-x2+bx+c经过A、B两点,并于x轴交于另一点C(点C在点A的右侧),点P是抛物线上一动点.
在平面直角坐标系中,直线y=x+4与x轴分别交于A、B两点,抛物线y=-x2+bx+c经过A、B两点,并于x轴交于另一点C(点C在点A的右侧),点P是抛物线上一动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
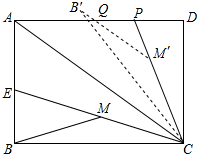 已知矩形ABCD中,AB=3,BC=4,CE平分∠ACB交AB于点E,M为CE的中点,连结BM,将△BCM绕点C顺时针旋转至△B′CM′,B′M′交AD于Q,延长CM′交AD于P,若PQ=PM′,则PQ=$\frac{25}{8}$-$\frac{2\sqrt{10}}{3}$.
已知矩形ABCD中,AB=3,BC=4,CE平分∠ACB交AB于点E,M为CE的中点,连结BM,将△BCM绕点C顺时针旋转至△B′CM′,B′M′交AD于Q,延长CM′交AD于P,若PQ=PM′,则PQ=$\frac{25}{8}$-$\frac{2\sqrt{10}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,lA、lB分别表示小明步行与小刚骑车在同一条路上行驶的路程S与时间t之间的关系.
如图,lA、lB分别表示小明步行与小刚骑车在同一条路上行驶的路程S与时间t之间的关系.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
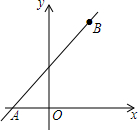 如图,在平面直角坐标系内,若一次函数y=kx+b的图象与x轴交于点A(-1,0),且经过点B(4,4),O为坐标原点,则cos∠BAO的值是$\frac{5\sqrt{41}}{41}$.
如图,在平面直角坐标系内,若一次函数y=kx+b的图象与x轴交于点A(-1,0),且经过点B(4,4),O为坐标原点,则cos∠BAO的值是$\frac{5\sqrt{41}}{41}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在⊙O中,弦AC、BD交于点E,弧AB=弧BC=弧CD.若∠BDC=25°,则∠ACD等于( )
如图,在⊙O中,弦AC、BD交于点E,弧AB=弧BC=弧CD.若∠BDC=25°,则∠ACD等于( )| A. | 60° | B. | 90° | C. | 105° | D. | 120° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com