
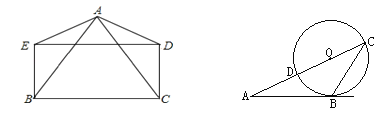
【题目】(1)已知:如图,四边形BCDE是矩形,AB=AC.求证:AE=AD
(2)如图,△ABC的边AC与⊙O相交于C、D两点,且经过圆心O,边AB与⊙O相切,切点为B. 若∠A=30°,求∠C
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】若△ABC中,BC=13,AC=5,AB=12,则下列判断正确的是( )
A. ∠A=90°B. ∠B=90°
C. ∠C=90D. △ABC是锐角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
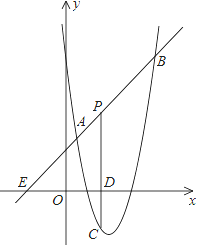
【题目】如图,直线![]() 与抛物线
与抛物线![]() 相交于A(
相交于A(![]() ,
,![]() )和B(4,
)和B(4,![]() ),点P是线段AB上异于A、B的动点,过点P作PC⊥
),点P是线段AB上异于A、B的动点,过点P作PC⊥![]() 轴于点D,交抛物线于点C.
轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)求△PAC为直角三角形时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果将某一抛物线向右平移2个单位,再向上平移2个单位后所得新抛物线的表达式是y=2(x-1)2,那么原抛物线的表达式是( )
A. y=2(x-3)2-2 B. y=2(x-3)2+2
C. y=2(x+1)2-2 D. y=2(x+1)2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
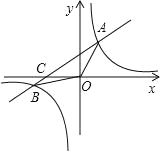
【题目】如图,已知反比例函数y=![]() 与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4).
与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4).
(1)试确定这两个函数的表达式;
(2)求出这两个函数图象的另一个交点B的坐标,并求△A0B的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com