
”¾ĢāÄæ”潫ijĄ×“ļ²āĖŁĒų¼ą²āµ½µÄŅ»×éĘū³µµÄŹ±ĖŁŹż¾ŻÕūĄķ£¬µĆµ½ĘäʵŹż·Ö²¼±ķ£ØĪ“Ķź³É£©£ŗ
Źż¾Ż¶Ī | 30”«40 | 40”«50 | 50”«60 | 60”«70 | 70”«80 | ×Ü¼Ę |
ʵ Źż | 10 | 40 | | | 20 | |
°Ł·Ö±Č | 5% | | 40% | | 10% | |
×¢£ŗ30”«40ĪŖŹ±ĖŁ“óÓŚµČÓŚ30Ē§Ć׶ųŠ”ÓŚ40Ē§Ć×£¬ĘäĖūĄąĶ¬£®
£Ø1£©ĒėÄć°Ń±ķÖŠµÄŹż¾ŻĢīŠ“ĶźÕū£»
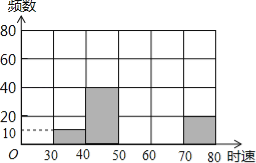
£Ø2£©²¹Č«ĘµŹż·Ö²¼Ö±·½Ķ¼£»
£Ø3£©Čē¹ū“ĖĀ·¶ĪĘū³µŹ±ĖŁ³¬¹ż60Ē§Ć×¼“ĪŖĪ„ÕĀ£¬ŌņĪ„ÕĀ³µĮ¾¹²ÓŠ¶ąÉŁĮ¾£æ
”¾“š°ø”æ£Ø1£©Ģī±ķ¼ū½āĪö£»£Ø2£©Ķ¼ŠĪ¼ū½āĪö£»£Ø3£©Ī„ÕĀ³µĮ¾¹²ÓŠ70Į¾£®
”¾½āĪö”æ
ŹŌĢā£Ø1£©ÓĆ30”«40µÄʵŹż³żŅŌ°Ł·Ö±ČĒó³ö×ÜʵŹż£¬Č»ŗó·Ö±š¼ĘĖćĒó³öĻąÓ¦µÄʵŹż»ņ°Ł·Ö±Č£¬Č»ŗóĢī±ķ¼“æÉ£»
£Ø2£©øł¾Ż£Ø1£©µÄŹż¾Ż²¹Č«Ö±·½Ķ¼¼“æÉ£»
£Ø3£©Ēó³öŗóĮ½×éµÄʵŹżÖ®ŗĶ¼“æÉ£®
ŹŌĢā½āĪö£ŗ£Ø1£©×ÜʵŹżĪŖ10”Ā5%=200£¬40”«50£¬![]() ”Į100%=20%£¬50”«60£¬200”Į40%=80£¬
”Į100%=20%£¬50”«60£¬200”Į40%=80£¬
200©10©40©80©20=50£¬![]() ”Į100%=25%£»
”Į100%=25%£»
Ģī±ķČēĻĀ£ŗ
Źż¾Ż¶Ī | 30”«40 | 40”«50 | 50”«60 | 60”«70 | 70”«80 | ×Ü¼Ę |
ʵ Źż | 10 | 40 | 80 | 50 | 20 | 200 |
°Ł·Ö±Č | 5% | 20% | 40% | 25% | 10% | 100% |
£Ø2£©²¹Č«ĘµŹż·Ö²¼Ö±·½Ķ¼ČēĶ¼ĖłŹ¾£»
£Ø3£©Ī„ÕĀ³µĮ¾¹²ÓŠ50+20=70£ØĮ¾£©£®



 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æa,b·Ö±šŹĒŹżÖįÉĻĮ½øö²»Ķ¬µÄµćA,BĖł±ķŹ¾µÄÓŠĄķŹż£¬ĒŅ![]() =5£¬
=5£¬![]() =2£¬A,BĮ½µćŌŚŹżÖįÉĻµÄĪ»ÖĆČēĶ¼ĖłŹ¾£ŗ
=2£¬A,BĮ½µćŌŚŹżÖįÉĻµÄĪ»ÖĆČēĶ¼ĖłŹ¾£ŗ
![]()
(1) ŹŌČ·¶ØŹża,b£»
(2) A£¬BĮ½µćĻą¾ą¶ąÉŁøöµ„Ī»³¤¶Č£æ
(3)ČōCµćŌŚŹżÖįÉĻ£¬CµćBµćµÄ¾ąĄėŹĒCµćµ½Aµć¾ąĄėµÄ![]() £¬ĒóCµć±ķŹ¾µÄŹż£»
£¬ĒóCµć±ķŹ¾µÄŹż£»
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌĶĮĻĀĮŠ²ÄĮĻ£ŗĪŅĆĒÖŖµĄ![]() µÄ¼øŗĪŅāŅåŹĒŌŚŹżÖįÉĻŹż
µÄ¼øŗĪŅāŅåŹĒŌŚŹżÖįÉĻŹż![]() ¶ŌÓ¦µÄµćÓėŌµćµÄ¾ąĄė£¬¼“
¶ŌÓ¦µÄµćÓėŌµćµÄ¾ąĄė£¬¼“![]() £¬Ņ²¾ĶŹĒĖµ£¬
£¬Ņ²¾ĶŹĒĖµ£¬![]() ±ķŹ¾ŌŚŹżÖįÉĻŹż
±ķŹ¾ŌŚŹżÖįÉĻŹż![]() ÓėŹż
ÓėŹż![]() ¶ŌÓ¦µćÖ®¼äµÄ¾ąĄė.Õāøö½įĀŪæÉŅŌĶĘ¹ćĪŖ£ŗ
¶ŌÓ¦µćÖ®¼äµÄ¾ąĄė.Õāøö½įĀŪæÉŅŌĶĘ¹ćĪŖ£ŗ![]() ±ķŹ¾ŌŚŹżÖįÉĻŹż
±ķŹ¾ŌŚŹżÖįÉĻŹż![]() Óė
Óė![]() ¶ŌÓ¦µćÖ®¼äµÄ¾ąĄė.
¶ŌÓ¦µćÖ®¼äµÄ¾ąĄė.
Ąż![]() ŅŃÖŖ
ŅŃÖŖ![]() £¬Ēó
£¬Ēó![]() µÄÖµ.
µÄÖµ.
½ā£ŗŌŚŹżÖįÉĻÓėŌµć¾ąĄėĪŖ![]() µÄµćµÄ¶ŌÓ¦ŹżĪŖ
µÄµćµÄ¶ŌÓ¦ŹżĪŖ![]() ŗĶ
ŗĶ![]() £¬¼“
£¬¼“![]() µÄÖµĪŖ
µÄÖµĪŖ![]() ŗĶ
ŗĶ![]() .
.
Ąż![]() ŅŃÖŖ
ŅŃÖŖ![]() £¬Ēó
£¬Ēó![]() µÄÖµ.
µÄÖµ.
½ā£ŗŌŚŹżÖįÉĻÓė![]() µÄ¾ąĄėĪŖ
µÄ¾ąĄėĪŖ![]() µćµÄ¶ŌÓ¦ŹżĪŖ
µćµÄ¶ŌÓ¦ŹżĪŖ![]() ŗĶ
ŗĶ![]() £¬¼“
£¬¼“![]() µÄÖµĪŖ
µÄÖµĪŖ![]() ŗĶ
ŗĶ![]() .
.
·ĀÕÕŌĶĮ²ÄĮĻµÄ½ā·Ø£¬½ā¾öĻĀĮŠĪŹĢā£ŗ
£Ø1£©ŅŃÖŖ![]() £¬Ēó
£¬Ēó![]() µÄÖµ£»
掙术
£Ø2£©ŅŃÖŖ![]() £¬Ēó
£¬Ēó![]() µÄÖµ£»
掙术
£Ø3£©ČōŹżÖįÉĻ±ķŹ¾![]() µÄµćŌŚ
µÄµćŌŚ![]() Óė
Óė![]() Ö®¼ä£¬Ōņ
Ö®¼ä£¬Ōņ![]() µÄÖµĪŖ_________£»
µÄÖµĪŖ_________£»
£Ø4£©µ±![]() Āś×ć_________Ź±£¬Ōņ
Āś×ć_________Ź±£¬Ōņ![]() µÄÖµ×īŠ”£¬×īŠ”ÖµŹĒ_________.
µÄÖµ×īŠ”£¬×īŠ”ÖµŹĒ_________.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijÉĢµź¹ŗ½ų¼×”¢ŅŅĮ½ÖÖÉĢĘ·£¬ŅŃÖŖĆ漞¼×ÖÖÉĢĘ·µÄ¼Ūøń±ČĆ漞ŅŅÖÖÉĢĘ·µÄ¼Ūøń¹ó10ŌŖ£¬ÓĆ350ŌŖ¹ŗĀņ¼×ÖÖÉĢĘ·µÄ¼žŹżĒ”ŗĆÓėÓĆ300ŌŖ¹ŗĀņŅŅÖÖÉĢĘ·µÄ¼žŹżĻąĶ¬£®
(1)Ēó¼×”¢ŅŅĮ½ÖÖÉĢĘ·Ć漞µÄ¼Ūøńø÷ŹĒ¶ąÉŁŌŖ£æ
(2)¼Ę»®¹ŗĀņÕāĮ½ÖÖÉĢĘ·¹²50¼ž£¬ĒŅĶ¶ČėµÄ¾·Ń²»³¬¹ż3200ŌŖ£¬ÄĒĆ“£¬×ī¶ąæɹŗĀņ¶ąÉŁ¼ž¼×ÖÖÉĢĘ·£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬øųÕżĪå±ßŠĪµÄ¶„µćŅĄ“Ī±ąŗÅĪŖ1£¬2£¬3£¬4£¬5£®Čō“ÓijŅ»¶„µćæŖŹ¼£¬ŃŲÕżĪå±ßŠĪµÄ±ßĖ³Ź±Õė·½ĻņŠŠ×ߣ¬¶„µć±ąŗÅµÄŹż×ÖŹĒ¼ø£¬¾Ķ×ß¼øøö±ß³¤£¬Ōņ³ĘÕāÖÖ×ß·ØĪŖŅ»“Ī”°ŅĘĪ»”±£®Čē£ŗŠ”ÓīŌŚ±ąŗÅĪŖ3µÄ¶„µćÉĻŹ±£¬ÄĒĆ“ĖūÓ¦×ß3øö±ß³¤£¬¼““Ó3”ś4”ś5”ś1ĪŖµŚŅ»“Ī”°ŅĘĪ»”±£¬ÕāŹ±Ėūµ½“ļ±ąŗÅĪŖ1µÄ¶„µć£»Č»ŗó“Ó1”ś2ĪŖµŚ¶ž“Ī”°ŅĘĪ»”±£®ČōŠ”Óī“Ó±ąŗÅĪŖ2µÄ¶„µćæŖŹ¼£¬µŚ15“Ī”°ŅĘĪ»”±ŗó£¬ŌņĖūĖł“¦¶„µćµÄ±ąŗÅĪŖ__£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗa”¢bĪŖÓŠĄķŹż£¬ĻĀĮŠĖµ·Ø£ŗ¢ŁČō a”¢b»„ĪŖĻą·“Źż£¬Ōņ![]() £»¢ŚČō
£»¢ŚČō![]() Ōņ
Ōņ![]() £»¢ŪČō
£»¢ŪČō![]() £¬Ōņ
£¬Ōņ![]() £»¢ÜČō
£»¢ÜČō![]() £¬Ōņ
£¬Ōņ![]() ŹĒÕżŹż.ĘäÖŠÕżČ·µÄÓŠ
ŹĒÕżŹż.ĘäÖŠÕżČ·µÄÓŠ
A.1øöB.2øöC.3øöD.4øö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼×”¢ŅŅĮ½³Ē¼äµÄĢśĀ·Ā·³ĢĪŖ1600Ē§Ć×£¬¾¹ż¼¼ŹõøÄŌģ£¬ĮŠ³µŹµŹ©ĮĖĢįĖŁ£¬ĢįĖŁŗó±ČĢįĖŁĒ°ĖŁ¶ČŌö¼ÓĮĖ20Ē§Ć×/Š”Ź±£¬ĮŠ³µ“Ӽ׳Ēµ½ŅŅ³ĒŠŠŹ»Ź±¼ä¼õÉŁ4Š”Ź±£¬ÕāĢõĢśĀ·ŌŚĻÖÓŠĢõ¼žĻĀ°²Č«ŠŠŹ»ĖŁ¶Č²»µĆ³¬¹ż140Ē§Ć×/Š”Ź±£¬ĒėÄćÓĆѧ¹żµÄÖŖŹ¶ĖµĆ÷ŌŚÕāĢõĢśĀ·µÄĻÖÓŠĢõ¼žĻĀĮŠ³µŹĒ·ń»¹æÉŅŌŌŁĢįĖŁ”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĄą±ČѧĻ°£ŗŅ»¶ÆµćŃŲ×ÅŹżÖįĻČĻņÓŅĘ½ŅĘ3øöµ„Ī»³¤¶Č£¬ŌŁĻņ×óĘ½ŅĘ2øöµ„Ī»³¤¶Č£¬Ļąµ±ÓŚĻņÓŅĘ½ŅĘ1øöµ„Ī»³¤¶Č£®ÓĆŹµŹż¼Ó·Ø±ķŹ¾ĪŖ3+£Ø-2£©=1£®Čō×ų±źĘ½ĆęÉĻµÄµćÓŠČēĻĀĘ½ŅĘ£ŗŃŲxÖį·½ĻņĘ½ŅʵďżĮæĪŖa£ØĻņÓŅĪŖÕż£¬Ļņ×óĪŖøŗ£¬Ę½ŅĘ|a|øöµ„Ī»³¤¶Č£©£¬ŃŲyÖį·½ĻņĘ½ŅʵďżĮæĪŖb£ØĻņÉĻĪŖÕż£¬ĻņĻĀĪŖøŗ£¬Ę½ŅĘ|b|øöµ„Ī»³¤¶Č£©£¬Ōņ°ŃÓŠŠņŹż¶Ō{a£¬b}½Š×öÕāŅ»Ę½ŅʵĔ°Ę½ŅĘĮæ”±£¬”°Ę½ŅĘĮæ”±{a£¬b}Óė”°Ę½ŅĘĮæ”±{c£¬d}µÄ¼Ó·ØŌĖĖć·ØŌņĪŖ{a£¬b}+{c£¬d}={a+c£¬b+d}£®
½ā¾öĪŹĢā£ŗ
(1)¼ĘĖć£ŗ{3,1}+{1,2},{1,2}+{3,1}.
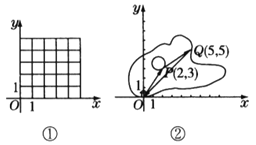
(2)¶ÆµćP“Ó×ų±źŌµćO³ö·¢£¬ĻČ°“ÕÕ”°Ę½ŅĘĮæ”±{3£¬1}Ę½Ņʵ½µćA£¬ŌŁ°“ÕÕ”°Ę½ŅĘĮæ”±{1£¬2}Ę½Ņʵ½µćB£»ČōĻČ°Ń¶ÆµćP°“ÕÕ”°Ę½ŅĘĮæ”±{1£¬2}Ę½Ņʵ½µćC£¬ŌŁ°“ÕÕ”°Ę½ŅĘĮæ”±{3£¬1}Ę½ŅĘ£¬×īŗóµÄĪ»ÖĆ»¹ŹĒµćBĀš£æŌŚĶ¼¢ŁÖŠ»³öĖıߊĪOABC.
(3)ČēĶ¼¢ŚĖłŹ¾£¬Ņ»ĖŅ“¬“ÓĀėĶ·O³ö·¢£¬ĻČŗ½ŠŠµ½ŗžŠÄµŗĀėĶ·P(2£¬3)£¬ŌŁ“ÓĀėĶ·Pŗ½ŠŠµ½ĀėĶ·Q(5£¬5)£¬×īŗó»Ųµ½³ö·¢µćO£®ĒėÓĆ”°Ę½ŅĘĮæ”±¼Ó·ØĖćŹ½±ķŹ¾ĖüµÄŗ½ŠŠ¹ż³Ģ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
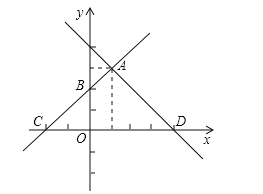
”¾ĢāÄæ”æŌŚČēĶ¼ĖłŹ¾µÄĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ö±ĻßAB£ŗy=k1x+b1ÓėÖ±ĻßAD£ŗy=k2x+b2Ļą½»ÓŚµćA£Ø1£¬3£©£¬ĒŅµćB×ų±źĪŖ£Ø0£¬2£©£¬Ö±ĻßAB½»xÖįøŗ°ėÖįÓŚµćC£¬Ö±ĻßAD½»xÖįÕż°ėÖįÓŚµćD£®
£Ø1£©ĒóÖ±ĻßABµÄŗÆŹż½āĪöŹ½£»
£Ø2£©Čō”÷ACDµÄĆ껿ĪŖ9£¬½ā²»µČŹ½£ŗk2x+b2£¾0£»
£Ø3£©ČōµćMĪŖxÖįŅ»¶Æµć£¬µ±µćMŌŚŹ²Ć“Ī»ÖĆŹ±£¬Ź¹AM+BMµÄÖµ×īŠ”£æĒó³ö“ĖŹ±µćMµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com