
【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中: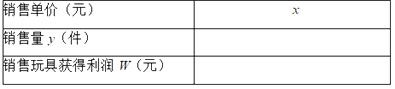
(2)在(1)条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
【答案】
(1)解:
销售单价(元) | x |
销售量y(件) | 1000-10x |
销售玩具获得利润w(元) | -10x2+1300x-30000 |
(2)解:-10x2+1300x-30000=10000
解之得:x1=50,x2=80
答:玩具销售单价为50元或80元时,可获得10000元销售利润,
(3)解:根据题意得
![]()
解之得:44≤x≤46,
w=-10x2+1300x-30000=-10(x-65)2+12250,
∵a=-10<0,对称轴是直线x=65,
∴当44≤x≤46时,w随x增大而增大.
∴当x=46时,W最大值=8640(元).
答:商场销售该品牌玩具获得的最大利润为8640元.
【解析】(1)销售量y=600-减少的数量,售该品牌玩具获得利润w=(每件的售价-进件)![]() 销售量y,即可求出结果。
销售量y,即可求出结果。
(2)根据w=10000,建立方程求解即可。
(3)建立不等式组:销售单价≥44,且y≥540,解不等式组,再根据二次函数的增减性,即可求出结果。


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
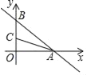
【题目】在平面直角坐标系中,已知一次函数y=﹣![]() x+6与x,y轴分别交于A,B两点,点C(0,n)是线段BO上一点,将△AOB沿直线AC折叠,点B刚好落在x轴负半轴上,则点C的坐标是( )
x+6与x,y轴分别交于A,B两点,点C(0,n)是线段BO上一点,将△AOB沿直线AC折叠,点B刚好落在x轴负半轴上,则点C的坐标是( )
A. (0,3) B. (0,![]() ) C. (0,
) C. (0,![]() ) D. (0,
) D. (0,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AC的表达式为y=![]() x+8,点P从点A开始沿AO向点O以1个单位/s的速度移动,点Q从点O开始沿OC向点C以2个单位/s的速度移动.如果P,Q两点分别从点A,O同时出发,经过几秒能使△PQO的面积为8个平方单位?
x+8,点P从点A开始沿AO向点O以1个单位/s的速度移动,点Q从点O开始沿OC向点C以2个单位/s的速度移动.如果P,Q两点分别从点A,O同时出发,经过几秒能使△PQO的面积为8个平方单位?

查看答案和解析>>
科目:初中数学 来源: 题型:
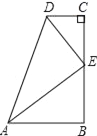
【题目】在数学活动课上,小明提出这样一个问题:如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 的坐标分别是点
的坐标分别是点![]() ,
,![]() ,且
,且![]() 满足:
满足:![]() .
.
(1)则![]() _________,
_________,![]() _________;
_________;
(2)![]() 为
为![]() 轴负半轴上一点,过点
轴负半轴上一点,过点![]() 作
作![]() 交
交![]() 轴于点
轴于点![]() .
.
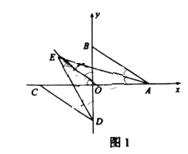
①如图1,![]() 与
与![]() 的角平分线交于点
的角平分线交于点![]() ,求
,求![]() 的度数;
的度数;
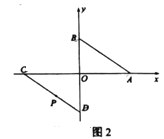
②如图2,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为线段
为线段![]() 上一点,求
上一点,求![]() 之间满足的关系式.
之间满足的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按![]() 元/公里计算,耗时费按
元/公里计算,耗时费按![]() 元/分钟计算(总费用不足
元/分钟计算(总费用不足![]() 元按
元按![]() 元计价).小敏、小刚两人用该打车方式出行,按上述计价规则,其行驶里程数、耗时以及打车总费用如下表:
元计价).小敏、小刚两人用该打车方式出行,按上述计价规则,其行驶里程数、耗时以及打车总费用如下表:
里程数 | 耗时 | 车费(元) | |
小敏 |
|
|
|
小刚 |
|
|
|
![]() 求
求![]() 的值;
的值;
![]() 若小华也用该打车方式打车,平均车速为
若小华也用该打车方式打车,平均车速为![]() 公里/时,行驶了
公里/时,行驶了![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com