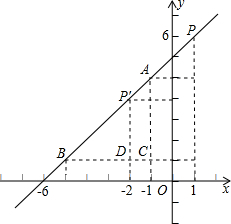
解:(1)把A(-1,b-1)、B(-5,b-5)两点代入y=

,得:
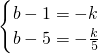
,
解得:
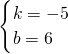
,
∴正比例函数解析式为:y=x+6,
反比例函数反比例函数解析式为:y=-

;
(2)∵直线AB为y=x+6,且A(-1,5),B(-5,1),
过点A,B分别作y轴、x轴的平行线,它们相交于点C(-1,1),
则AC=BC=4,
①P点在线段AB上时,作PE∥BC,交AC于E,作PD∥AC交BC于D,
则
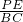
=

,
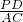
=

,
∵
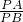
=

,
∴

=

,

=

,
∴PE=1,PD=3,
∴P(-2,4),
∴抛物线的解析式为:y=-(x-1)
2+4,
即y=-x
2-4x,
此时,c=0,不符合题意,舍去;
②当P点在线段BA的延长线上时,同理可得:P(1,7)
∴抛物线的解析式为:y=-(x-1)
2+7,
即y=-x
2+2x+6,
此时,c=6>0,符合题意,
∴由①、②可知,抛物线的解析式为:y=-x
2+2x+6;
(3)设平移后的直线解析式为:y=x+t,
它交x轴于点(-t,0),交y轴于点(0,t),
∴S
△=

×|-t|×|t|=2,
∴t=±2,
∴平移后的直线解析式为:y=x+2或y=x-2,
即图象向右平移了4个单位或8个单位,
此时的抛物线解析式为:y=-(x-1-4)
2+7或y=-(x-1-8)
2+7,
即y=-x
2+10x-18或y=-x
2+18x-74.
分析:(1)利用待定系数法求出一次函数解析式和反比例函数解析式即可;
(2)根据P点在线段AB上时,作PE∥BC,交AC于E,作PD∥AC交BC于D或当P点在线段BA的延长线上时,利用平行线的性质分别求出即可;
(3)首先求出直线解析式,进而得出抛物线解析式即可.
点评:此题主要考查了反比例函数的综合应用以及二次函数解析式的求法和平行线分线段成比例定理等知识,正确得出直线AB解析式是解题关键.

 (k≠0)的图象与一次函数y=x+b的图象交于A(-1,b-1)、B(-5,b-5)两点.
(k≠0)的图象与一次函数y=x+b的图象交于A(-1,b-1)、B(-5,b-5)两点.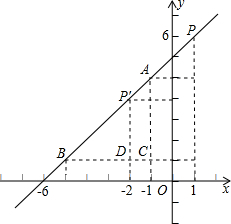 解:(1)把A(-1,b-1)、B(-5,b-5)两点代入y=
解:(1)把A(-1,b-1)、B(-5,b-5)两点代入y= ,得:
,得: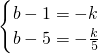 ,
,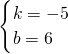 ,
, ;
;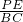 =
= ,
,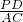 =
= ,
,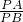 =
= ,
, =
= ,
, =
= ,
, ×|-t|×|t|=2,
×|-t|×|t|=2,


 如图,在平面直角坐标中,已知直线y=kx+b与直线y=
如图,在平面直角坐标中,已知直线y=kx+b与直线y= 如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=
如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数y=