
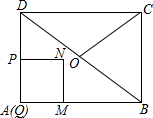
 如图1,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD-DO以每秒1个单位长度的速度向终点O运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).
如图1,在矩形ABCD中,AB=4,BC=3,点O为对角线BD的中点,点P从点A出发,沿折线AD-DO以每秒1个单位长度的速度向终点O运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).分析 (1)可证△DPN∽△DQB,从而有 $\frac{DP}{DQ}$=$\frac{PN}{QB}$,即可求出t的值.
(2)只需考虑两个临界位置(①MN经过点O,②点P与点O重合)下t的值,即可解决问题.
(3)根据正方形PQMN与△ABD重叠部分图形形状不同分成三类,如图4、图5,图6,然后运用三角形相似、锐角三角函数等知识就可求出S与t之间的函数关系式.
解答 解:(1)当点N落在BD上时,如图1.
∵四边形PQMN是正方形,
∴PN∥QM,PN=PQ=t.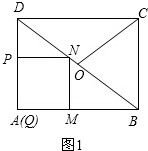
∴△DPN∽△DQB.
∴$\frac{DP}{DQ}$=$\frac{PN}{QB}$,
∵PN=PQ=PA=t,DP=3-t,QB=AB=4,
∴$\frac{3-t}{3}$=$\frac{t}{4}$,
∴t=$\frac{12}{7}$.
∴当t=$\frac{12}{7}$s时,点N落在BD上.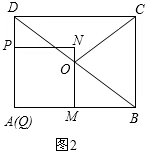
(2)①如图2,
则有QM=QP=t,MB=4-t.
∵四边形PQMN是正方形,
∴MN∥DQ.
∵点O是DB的中点,
∴QM=BM.
∴t=4-t.
∴t=2.
②如图3,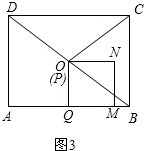
∵四边形ABCD是矩形,
∴∠A=90°.
∵AB=4,AD=3,
∴DB=5.
∵点O是DB的中点,
∴DO=$\frac{5}{2}$,
∴1×t=AD+DO=3+$\frac{5}{2}$.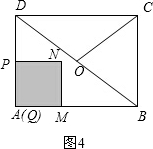
∴t=$\frac{11}{2}$.
∴当t=4s或11s时,正方形PQMN的边经过点O.
(3)①当0<t≤$\frac{12}{7}$时,如图4.
S=S正方形PQMN=PQ2=PA2=t2.
②当 $\frac{12}{7}$<t≤3时,如图5,
∵tan∠ADB=$\frac{PG}{DP}$=$\frac{AB}{AD}$,
∴$\frac{PG}{3-t}$=$\frac{4}{3}$,
∴PG=4-$\frac{4}{3}$t.
∴GN=PN-PG=t-(4-$\frac{4}{3}$t)=$\frac{7}{3}$t-4,
∵tan∠NFG=tan∠ADB=$\frac{4}{3}$,
∴$\frac{GN}{NF}$=$\frac{4}{3}$,
∴NF=$\frac{3}{4}$GN=$\frac{3}{4}$( $\frac{7}{3}$t-4)=$\frac{7}{4}$t-3.
∴S=S正方形PQMN-S△GNF
=t2-$\frac{1}{2}$×( $\frac{7}{3}$t-4)×( $\frac{7}{4}$t-3)=-$\frac{24}{25}$t2+7t-6.
综上所述:当0<t≤$\frac{12}{7}$时,S=t2.
当 $\frac{12}{7}$<t≤3时,S=-$\frac{24}{25}$t2+7t-6.
③当3<t≤$\frac{11}{2}$时,如图6,
∵四边形PQMN是正方形,四边形ABCD是矩形.
∴∠PQM=∠DAB=90°.
∴PQ∥AD.
∴△BQP∽△BAD.
∴$\frac{BP}{BD}$=$\frac{BQ}{BA}$=$\frac{PQ}{AD}$,
∵BP=8-t,BD=5,BA=4,AD=3,
∴$\frac{8-t}{5}$=$\frac{BQ}{4}$=$\frac{PQ}{3}$,
∴BQ=$\frac{4(8-t)}{5}$,PQ=$\frac{3(8-t)}{5}$,
∴QM=PQ=$\frac{3(8-t)}{5}$,
∴BM=BQ-QM=$\frac{8-t}{5}$,
∵tan∠ABD=$\frac{FM}{BM}$=$\frac{AD}{AB}$=$\frac{3}{4}$,
∴FM=$\frac{3}{4}$BM=$\frac{3(8-t)}{20}$,
∴S=S梯形PQMF=$\frac{1}{2}$(PQ+FM)•QM
=$\frac{1}{2}$[$\frac{3(8-t)}{5}$+$\frac{3(8-t)}{20}$]•$\frac{3(8-t)}{5}$=$\frac{9}{40}$(8-t)2
=$\frac{9}{40}$t2-$\frac{18}{5}$t+$\frac{72}{5}$.
点评 本题考查了矩形的性质、正方形的性质、相似三角形的判定与性质、锐角三角函数的定义、三角形的中位线定理、勾股定理等知识,考查了用割补法求五边形的面积,考查了用临界值法求t的取值范围,考查了分类讨论的数学思想,综合性较强.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
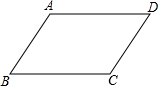 对四边形ABCD加条件,使之成为平行四边形,下面的添加不正确的是( )
对四边形ABCD加条件,使之成为平行四边形,下面的添加不正确的是( )| A. | AB=CD,AB∥CD | B. | AB∥CD,AD=BC | C. | AB=CD,AD=BC | D. | AC与BD相互平分 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-4)2=31 | B. | (x-4)2=1 | C. | (x-8)2=1 | D. | (x-8)2=31 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
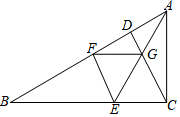 如图,在直角△ABC中,∠ACB=Rt∠,∠B=30°,CD为斜边AB上的高线,折叠△ABC使得AC落在AB上,点C与点F重合,展开的折痕AE交CD于点G,连接FG、EF.下列结论:①图中有6对全等三角形;②BC=6DG;③若将△EFG沿FG所在的直线折叠,则点E必在直线CD上;④AG=EF;⑤图中共有5个等腰直角三角形,其中正确的结论的个数是( )
如图,在直角△ABC中,∠ACB=Rt∠,∠B=30°,CD为斜边AB上的高线,折叠△ABC使得AC落在AB上,点C与点F重合,展开的折痕AE交CD于点G,连接FG、EF.下列结论:①图中有6对全等三角形;②BC=6DG;③若将△EFG沿FG所在的直线折叠,则点E必在直线CD上;④AG=EF;⑤图中共有5个等腰直角三角形,其中正确的结论的个数是( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 cm | B. | 10 cm | C. | 20 cm | D. | 40 cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 成绩(分) | 50 | 60 | 70 | 80 | 90 | 100 |
| 人数 | 2 | 6 | 9 | 18 | 13 | 2 |
| 成绩(分) | 50 | 60 | 70 | 80 | 90 | 100 |
| 人数 | 6 | 9 | 7 | 9 | 15 | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com