
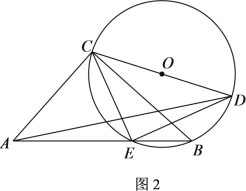
【题目】如图1,点E为△ABC边AB上的一点,⊙O为△BCE的外接圆,点D为![]() 上任意一点.若AE=AC=2n,BC=n2-1,BE=n2-2n+1 .(n≥2,且n为正整数) .
上任意一点.若AE=AC=2n,BC=n2-1,BE=n2-2n+1 .(n≥2,且n为正整数) .
(1)求证:∠CAE+∠CDE=90°;
(2)①如图2,当CD过圆心O时,①将△ACD绕点A顺时针旋转得△AEF,连接DF,请补全图形,猜想CD、DE、DF之间的数量关系,并证明你的猜想;②若n=3,求AD的长.

【答案】(1)证明见解析;(2)①补全图形见解析;![]() ,证明见解析;②
,证明见解析;②![]()
【解析】
(1)先计算AB的长,再根据勾股定理的逆定理判定![]() ,然后根据直角三角形的性质和圆周角定理的推论即可证得结论;
,然后根据直角三角形的性质和圆周角定理的推论即可证得结论;
(2)①根据题意即可补全图形,如图3,由旋转的性质得:![]() ,然后根据(1)的结论、四边形的内角和和周角的定义即可推出
,然后根据(1)的结论、四边形的内角和和周角的定义即可推出![]() ,再根据勾股定理和等量代换即可得出结论;
,再根据勾股定理和等量代换即可得出结论;
②如图4,过点![]() 作
作![]() 于
于![]() ,先根据△ABC的面积求出CH的长,再根据勾股定理和线段的和差关系求出AH和HE的长,进而可求出CE的长,由
,先根据△ABC的面积求出CH的长,再根据勾股定理和线段的和差关系求出AH和HE的长,进而可求出CE的长,由![]() 可得其正弦相等,进而可求出CD的长,然后由①的结论可求出DF的长,又易证
可得其正弦相等,进而可求出CD的长,然后由①的结论可求出DF的长,又易证![]() ,然后根据相似三角形的性质即可求出AD的长.
,然后根据相似三角形的性质即可求出AD的长.
(1)证明:![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
即![]() ;
;
(2)解:①补全图形如图3所示;
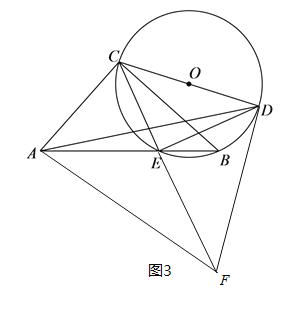
CD、DE、DF之间的数量关系是:![]() ,理由如下:
,理由如下:
如图 3,由旋转的性质得:![]() ,
,
由(1)得:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
②当![]() 时,
时,![]() ,
,
如图4,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
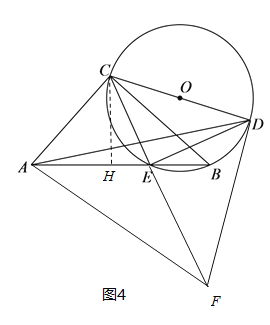
则由△ABC的面积可得:![]() ,
,
 ,
,
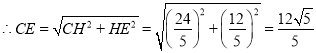 ,
,
∵CD是直径,∴∠CED=90°,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,即:
,即: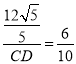 ,解得
,解得![]() ,
,
∴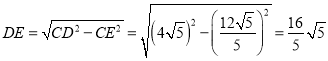 ,
,
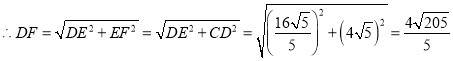 ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
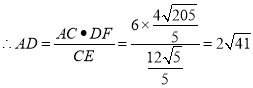 .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=5,以B为圆心BC为半径画弧交AD于点E,连接CE,作BF⊥CE,垂足为F,则tan∠FBC的值为( )
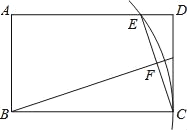
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线![]() 交坐标轴于A、C两点,抛物线
交坐标轴于A、C两点,抛物线![]() 过A、C两点.
过A、C两点.
(1)求抛物线的解析式;
(2)若点P为抛物线位于第三象限上一动点,连接PA,PC,试问△PAC是否存在最大值,若存在,请求出△APC取最大值以及点P的坐标,若不存在,请说明理由;
(3)点M为抛物线上一点,点N为抛物线对称轴上一点,若△NMC是以∠NMC为直角的等腰直角三角形,请直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
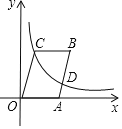
【题目】已知:如图,在平面直角坐标系xOy中,点A在x轴的正半轴上,点B、C在第一象限,且四边形OABC是平行四边形,AB=![]() ,sinB=
,sinB=![]() ,反比例函数
,反比例函数![]() 的图象经过点C以及边AB的中点D,则四边形OABC的面积为_____.
的图象经过点C以及边AB的中点D,则四边形OABC的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCO为矩形,点A在反比例函数y=![]() (x>0)的图象上,点C在反比例函数y=-
(x>0)的图象上,点C在反比例函数y=-![]() (x<0)的图象上,若点B在y轴上,则点A的坐标为_______.
(x<0)的图象上,若点B在y轴上,则点A的坐标为_______.
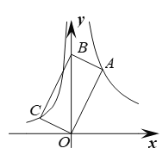
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y = x2 – 2 m x – 2m – 2与直线y =-x-2 交于C,D两点,将抛物线在C、D两点之间的部分(不含C、D)上恰有两个点的横坐标为整数,则m的取值范围为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子里装有两个红球,两个白球和一个蓝球,这些球除颜色外都相同.从中随机摸出一个球,记下颜色后放回,再从中随机摸出一个球,两次摸到的球的颜色能配成紫色(红色和蓝色能配成紫色)的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC边长是定值,点O是它的外心,过点O任意作一条直线分别交AB,BC于点D,E.将△BDE沿直线DE折叠,得到△B′DE,若B′D,B′E分别交AC于点F,G,连接OF,OG,则下列判断错误的是( )
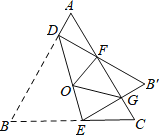
A. △ADF≌△CGE
B. △B′FG的周长是一个定值
C. 四边形FOEC的面积是一个定值
D. 四边形OGB'F的面积是一个定值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】攀枝花得天独厚,气候宜人,农产品资源极为丰富,其中晚熟芒果远销北上广等大城市.某水果店购进一批优质晚熟芒果,进价为10元/千克,售价不低于15元/千克,且不超过40元/每千克,根据销售情况,发现该芒果在一天内的销售量![]() (千克)与该天的售价
(千克)与该天的售价![]() (元/千克)之间的数量满足如下表所示的一次函数关系.
(元/千克)之间的数量满足如下表所示的一次函数关系.
销售量 | … | 32.5 | 35 | 35.5 | 38 | … |
售价 | … | 27.5 | 25 | 24.5 | 22 | … |
(1)某天这种芒果售价为28元/千克.求当天该芒果的销售量
(2)设某天销售这种芒果获利![]() 元,写出
元,写出![]() 与售价
与售价![]() 之间的函数关系式.如果水果店该天获利400元,那么这天芒果的售价为多少元?
之间的函数关系式.如果水果店该天获利400元,那么这天芒果的售价为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com