
����Ŀ����ͼ����һ�ų���a������b�ij�����Ӳֽ������ܸ���ȥһ���߳�Ϊc�������Σ�a��b��2c�������ۺϳ�һ���ǵij�������ӣ�ֽ��ĺ�Ⱥ��Բ��ƣ���
��1����a=12��b=7��c=2�����ۺϳɵij�������ӵIJ�����Ƕ��٣�
��2�����ú�a��b��c�Ĵ���ʽ��ʾ�۳ɵij�������ӵĵ����ܳ���
��3������ѳ�����Ӳֽ������ܼ�ȥ2���߳�Ϊc�������κ�2��ͬ����״��ͬ����С�ij����Σ�Ȼ���ۺϳ�һ���иǵij�������ӣ���ô���ĵ����ܳ��Ƕ��٣����ú�a��b��c�Ĵ���ʽ��ʾ��

���𰸡���1��44����2��2a+2b��8c����3��a+2b��6c��2a+b��4c��
��������
��1����![]() ʱ���ֱ������������ӵij��������ߣ�������������.
ʱ���ֱ������������ӵij��������ߣ�������������.
��2���ú�![]() �Ĵ���ʽ��ʾ�۳ɵij�������ӵ���ij���������ɱ�ʾ�������ܳ�.
�Ĵ���ʽ��ʾ�۳ɵij�������ӵ���ij���������ɱ�ʾ�������ܳ�.
��3�����������������ʾ��ͼ���ֱ���⼴��.
��1����![]() ʱ,��������ӵij�Ϊ��
ʱ,��������ӵij�Ϊ��![]() ��Ϊ��
��Ϊ��![]() ��Ϊ2.
��Ϊ2.
�ۺϳɵij�������ӵIJ�����ǣ�![]()
![]() ��������ӵĵ���ij�Ϊ��
��������ӵĵ���ij�Ϊ��![]() ��Ϊ��
����![]()
�۳ɵij�������ӵĵ����ܳ�Ϊ��![]()
��3��

����ͼ1��ʾ�ķ������ۣ�
�����ܳ�Ϊ��![]()
����ͼ2��ʾ�ķ������ۣ�
�����ܳ�Ϊ��![]()


 ��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���A��x���������ϣ�����C������Ϊ��4��3����D��������y=��x2+6x��һ�㣬����x���Ϸ������BCD��������ֵΪ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�����κ���y=ax2+bx+c��ͼ���У�����ͬѧ�۲�ó�������������Ϣ����1��b2��4ac��0����2��c��1����3��2a��b��0����4��a+b+c��0�����д�����У� ��
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ���ı���ABCD��һ���ǵ�ƽ���߰�һ���߷ֳɳ���4cm��5cm�������߶Σ���ƽ���ı���ABCD���ܳ���__________cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]() ����С����λ����������
����С����λ����������![]() ��
��![]() ����
����![]() ��ش����⣺
��ش����⣺
��1����ֱ��д��![]() ��
��![]() ��
��![]() ��ֵ��
��ֵ��![]()
![]()
![]()
��2����������![]() ��
��![]() ��
��![]() ����Ӧ�ĵ�ֱ�Ϊ
����Ӧ�ĵ�ֱ�Ϊ![]() ��
��![]() ��
��![]()
�ټ�![]() ��
��![]() �����ľ���Ϊ
�����ľ���Ϊ![]() ����
����![]() ��
��![]() ��
��
�ڵ�![]() Ϊ������Ķ��㣬���Ӧ����Ϊx����
Ϊ������Ķ��㣬���Ӧ����Ϊx����![]() �ڵ�
�ڵ�![]() ���
���![]() ֮���˶�ʱ�������˵㣩����
֮���˶�ʱ�������˵㣩����![]() ��
��![]() .
.
��3���ڣ�1����2�������£�����![]() ��
��![]() ��������ÿ��
��������ÿ��![]() ����λ���ȵ��ٶ����
����λ���ȵ��ٶ����![]() �ƶ�������
�ƶ�������![]() �˶���
�˶���![]() ��ʱ����
��ʱ����![]() ��
��![]() ��������ÿ��
��������ÿ��![]() ����λ������
����λ������![]() ���˶�����M��
���˶�����M��![]() ����
����![]() ���������������ͬ�����ٶȷ��ص�
���������������ͬ�����ٶȷ��ص�![]() . ���
. ���![]() �ƶ�ʱ��Ϊ
�ƶ�ʱ��Ϊ![]() �룬����
�룬����![]() ��ʼ�˶������ú�
��ʼ�˶������ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() ��
��![]() �����ľ���.
�����ľ���.
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijС��ƻ���һ�����й����������ÿ����5������ô�ȼƻ�����9�������ÿ����4������ô�ȼƻ���15������С�鹲�ж����ˣ��ƻ������ٸ����й�������
�������⣬С����С��ֱ��г����в������ķ������£�
С����5x����������=4x������������ С�죺![]() ��
��
��1������С����С�����еķ��̣���������������������ţ��������������������֣�����ֱ�ָ��δ֪��x��y��ʾ�����壮
С�����еķ�����x��ʾ�� ����
С�����еķ�����y��ʾ�� ����
��2����ѡ��С����С��������һ�ַ����������Ľ�����Ŀ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̴�λ�������㷨ͳ�ڡ���һ���й���ͳ��ѧ��Ҫ���������ڡ��㷨ͳ�ڡ��м��أ���ƽ����ǧδ��̤�����һ�ߣ����ж��������룬����˸����ǣ���Ů�����������ճ�Ц�ﻶ�ң�������ʿ�غ��棬��������м�������ע�͡�1��=5�ߣ�
���ģ�������ǧ��ֹʱ����ǧ�ϵ�̤�������1�߸ߣ��罫��ǧ��̤����ǰ�ƶ�������10�ߣ�ʱ��̤��ͺ���һ���ߣ���֪�����������5�ߣ������Ĺ���Ͳ����ǣ�ÿ�춼��������ǧ������Ц�����ղ��ϣ�������ܹ��ɽ������������ǧ���������Ƕ����𣿡�
��ͼ��������ǧ��������ʼ�ձ���ֱ��״̬��OA����ǧ�ľ�ֹ״̬��A��̤�壬CD�ǵ��棬��B���ƶ�������̤���λ�ã���AB��̤���ƶ��Ĺ켣����֪AC=1�ߣ�CD=EB=10�ߣ��˵�����BD=5�ߣ���������OA=OB=x�ߣ�����з���Ϊ �� 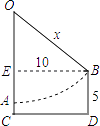
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������A��B�����Ӧ���ֱ�Ϊ-2��5��PΪ������һ�㣬��Ӧ��Ϊx��
��1����PΪ�߶�AB�����ȷֵ㣨��һ���߶�ƽ���ֳ���ȵ������ֵ������㣩����P���Ӧ������
��2���������Ƿ���ڵ�P��ʹP�㵽A�㣬B������Ϊ10�������ڣ����xֵ���������ڣ���˵�����ɣ�
��3������A����B�͵�P��P����ԭ�㣩ͬʱ�����˶������ǵ��ٶȷֱ�Ϊ1��6��3�����ȵ�λ/�֣���ڼ�����ʱ��A��B��P�����У�����һ���������������ɵ��߶ε��е㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
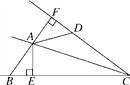
����Ŀ����ͼ��ACƽ�֡�BCD��AB��AD��AE��BC��E��AF��CD��F.
(1)����ABE��60�������CDA�Ķ�����
(2)��AE��2��BE��1��CD��4.���ı���AECD�������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com